Minitab 22 - Äquivalenztest, 2 Stichproben - Konfidenzintervalle - 1-α vs. 1-2α - Warum sind diese manchmal gleich und wann unterscheiden sie sich bei den beiden Methoden?
- Erstellt am 10.11.2025
- Software: Minitab 22
Wir erläutern die beiden Fragen in diesem Artikel an Hand von zwei Beispielen.
Bilder
|
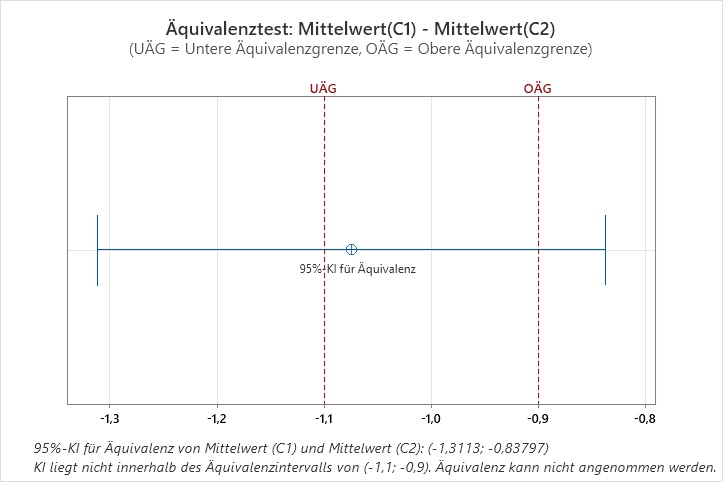
Bild 1: (100-5)%-Konfidenzintervall mit Äquivalenzintervall (-1,1: -0,9) |
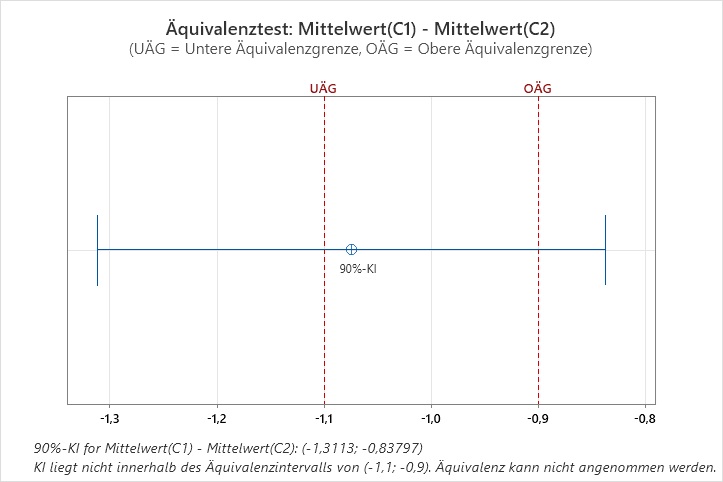
Bild 2: (100-2*5)%-Konfidenzintervall mit Äquivalenzintervall (-1,1: -0,9) |
|
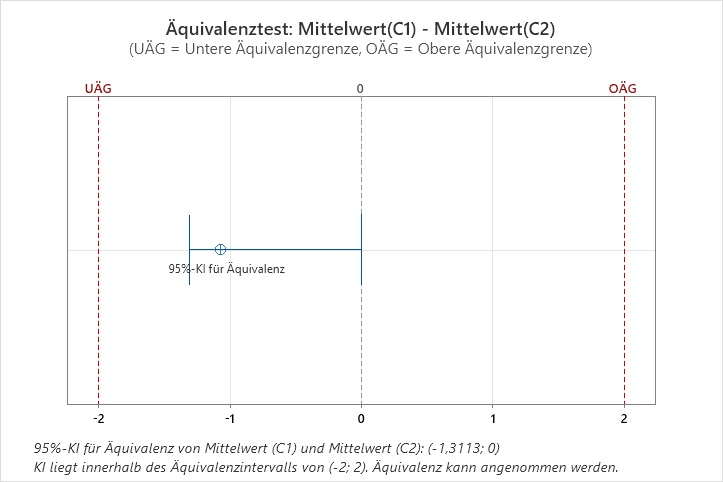
Bild 3: (100-5)%-Konfidenzintervall mit Äquivalenzintervall (-2: -2) |
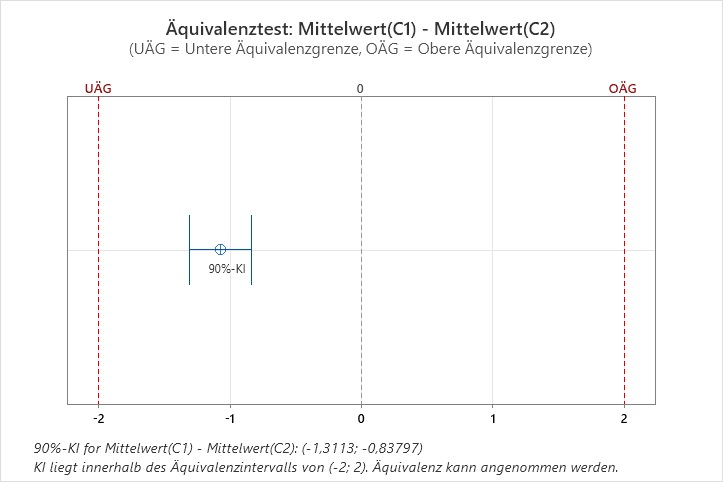
Bild 4: (100-2*5)%-Konfidenzintervall mit Äquivalenzintervall (-2: 2) |
Erläuterung
Für alle dargestellten Äquivalenzdiagramme wurde der gleiche Datensatz und das gleiche Signifikanzniveau verwendet. Die Mittelwertdifferenz der beiden Datensätze beträgt -1,0746. Wenn ein Konfidenzintervall komplett auf einer Seite des Mittelpunkts liegt, wird bei der Standardmethode die jeweils näher liegende Grenze auf den Mittelpunkt gesetzt.
Beispiel 1 - Bilder 1 und 2
- Der Äquivalenzbereich ist (-1,1; -0,9).
- Der Mittelpunkt des Äquivalenzbereichs liegt bei -1.
- Das Konfidenzintervall liegt hier so, dass seine Untergrenze unterhalb und seine Obergrenze oberhalb des Mittelpunkts liegt.
- In diesem Fall wird bei der Standardmethode die Grenze nicht auf den Mittelpunkt gesetzt.
Beide Methoden führen daher zum gleichen Ergebnis.
|
Äquivalenztest, 2 Stichproben: C1, C2 Methode Testmittelwert = Mittelwert von C1 Deskriptive Statistik
Differenz: Mittelwert(C1) - Mittelwert(C2)
KI liegt nicht innerhalb des Äquivalenzintervalls. Äquivalenz kann nicht angenommen werden. Test
Der größere der beiden p-Werte ist 0,430. Äquivalenz kann nicht angenommen werden. |
Äquivalenztest, 2 Stichproben: C1, C2 Methode Testmittelwert = Mittelwert von C1 Deskriptive Statistik
Differenz: Mittelwert(C1) - Mittelwert(C2)
KI liegt nicht innerhalb des Äquivalenzintervalls. Äquivalenz kann nicht angenommen werden. Test
Der größere der beiden p-Werte ist 0,430. Äquivalenz kann nicht angenommen werden. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Beispiel 2 - Bilder 3 und 4
- Der Äquivalenzbereich ist (-2; 2).
- Der Mittelpunkt des Äquivalenzbereichs liegt bei 0.
- Das Konfidenzintervall liegt vollständig unterhalb des Mittelpunkts des Äquivalenzbereichs.
- In diesem Fall wird bei der Standardmethode die Grenze auf den Mittelpunkt gesetzt.
Daher führen in diesem Beispiel die beiden Methoden zu unterschiedlichen Ergebnissen.
|
Äquivalenztest, 2 Stichproben: C1, C2 Methode Testmittelwert = Mittelwert von C1 Deskriptive Statistik
Differenz: Mittelwert(C1) - Mittelwert(C2)
KI liegt innerhalb des Äquivalenzintervalls. Äquivalenz kann angenommen werden. Test
Der größere der beiden p-Werte ist 0,000. Äquivalenz kann angenommen werden. |
Äquivalenztest, 2 Stichproben: C1, C2 Methode Testmittelwert = Mittelwert von C1 Deskriptive Statistik
Differenz: Mittelwert(C1) - Mittelwert(C2)
KI liegt innerhalb des Äquivalenzintervalls. Äquivalenz kann angenommen werden. Test
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|