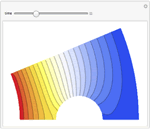
PDEs and Finite Elements
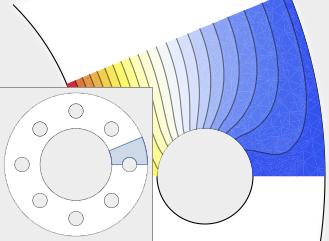
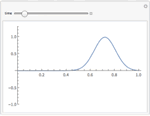
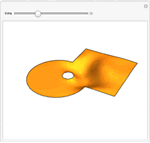
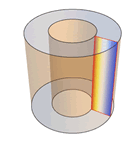
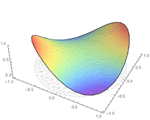
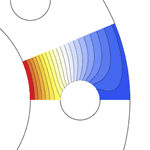
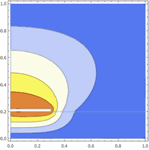
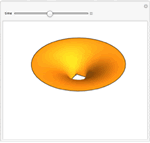
Mathematica Version 10 extends its numerical differential equation-solving capabilities to include the finite element method. Given a PDE, a domain, and boundary conditions, the finite element solution process - including grid and element generation - is fully automated. Stationary and transient solutions to a single PDE or a system of partial differential equations are supported for one, two, and three dimensions.
|
|