Branchenbezogene Anwendungsbeispiele des Wolfram SystemModelers Develop realistic models and digital twins for any industry with System Modeler. Core built-in components and custom libraries can represent elements and processes in any domain. Download a trial to experiment with the dynamic models yourself. Aerospace & Defense Automotive & Transportation Heavy Equipment Industrial Manufacturing Consumer Products Energy Life Sciences Business Other Aerospace & Defense Model and test complex systems such as unmanned aerial vehicles (UAV), space robotics, and aircraft dynamics. SystemModeler enables system- and component-level design and continuous testing and verification. 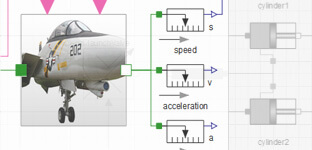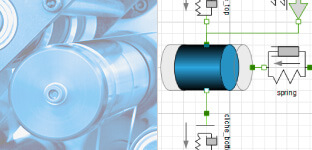Aircraft Catapult Model a hydraulic aircraft catapult to accelerate an aircraft to a high speed in a short distance. 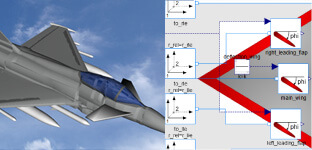See Example Fighter Create a library for aircraft modeling, which can be used to study flight dynamics during different flight conditions. See Example Satellite Model a satellite with a combination of 3D mechanics and block-based control logic and visualize the path for the satellite. See Example Flap System Reliability: Cessna 441 Compute the reliability of a Cessna 441 flap system using lifetime data for the individual hydraulic parts. See Example Automotive & Transportation Design and simulate vehicle dynamics, powertrain controllers, chassis and safety systems, and more with SystemModeler. Combine with Mathematica for control system design and optimization. Cruise control Import an FMU of a cruise control model from Simulink and evaluate its performance in a car model in Wolfram SystemModeler. 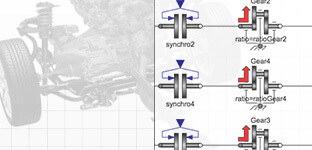See Example Driveline This example explores how the transmission control unit parameters affect fuel consumption for a midsize car. 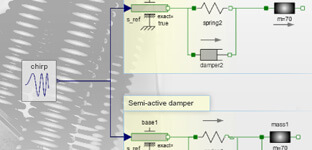See Example Truck Seat Suspension Model an active damper and compare with a passive damper in the driver's seat of a heavy truck. See Example Cam Design Design and prototype mechanisms such as cams with the symbolic component creation capabilities in SystemModeler. See Example Heavy Equipment Excavator Explore the reachable positions of an excavator's bucket and visualize the movement. See Example Active Damping Minimize vibrations in a diesel engine using a tuned mass damper. See Example Hydraulic Motor Study the effect of changing displacement in a hydraulic motor. See Example Model Inversion Control of a Hoist Crab In this example, a model of a hoist crab is used to demonstrate the application of model inversion control in controlling nonlinear systems. See Example Industrial Manufacturing Model new manufacturing processes prior to implementation or existing ones in order to diagnose problems. Use Mathematica for analyses including pre- and post-processing of models, simulations, and results. Industrial Robot Find the optimal way between two points for an industrial robot arm. See Example Printing Press Analyze configurations in which bouncing of the cylinders occurs in a flexographic printing press. See Example Continuously Stirred Tank Reactor Find an optimal control signal for a continuously stirred tank reactor (CSTR), while obeying safety limitations in temperature. 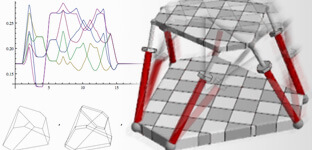See Example Stewart Platform Analyze the movement of a parallel manipulator and visualize its path in 3D. See Example Consumer Products Design home appliances and other electronics systems with SystemModeler and easily incorporate non-electronic elements, such as mechanical assemblies and temperature control, into the complete design. Joystick Design Compare three designs for a spring-based recentering mechanism in an analog joystick. 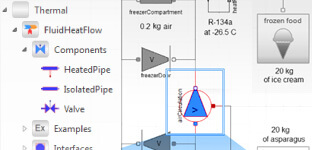See Example Refrigerator Freezer Simulate a household refrigerator freezer in several scenarios, including handling events such as the sudden triggering of a thermostat. See Example Electric Kettle Simulate a controlled heating process in a water heater. Combine components from multiple domains and identify parameters. See Example Energy Use SystemModeler to develop accurate models of wind, solar, and other power generation and distribution systems. Combine with Mathematica for further optimization and analysis. House Heating Compare energy consumption for house heating needs in different locations using measurement data. 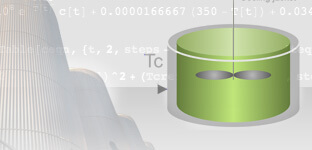See Example Battery This model allows you to analyze how a battery responds to thermal conditions as well as to charge and discharge cycles. See Example Life Sciences Use SystemModeler for modeling and analysis throughout drug discovery, development, clinical trials, and manufacturing. The flexible environment supports application areas such as systems biology, bioinformatics, and more. Meal Simulation Simulates the process that maintains healthy blood glucose levels in the human body after eating a meal. See Example Insulin Signaling Model a biochemical process and study how insulin signaling in fat cells works. See Example Estimating Liver Function Create a pharmacokinetic model to describe the distribution and transfer rates of contrast agent between different parts of the body. See Example An Influenza Epidemic Model the spread of an influenza virus in a population with components from the SystemDynamics library. See Example Business Enhance managerial understanding by using Wolfram System Modeler to simulate dynamic models of strategic business, economics and public policy issues. Production Chain Model a production chain for a company producing a durable good. 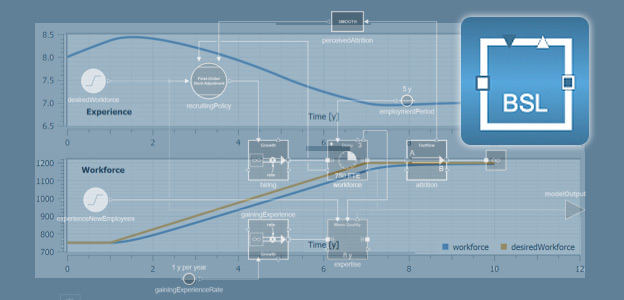See Example Employee Management Vary the control parameters that relate to aspects of the human resource planning (HRP) process to test different HRP strategies. 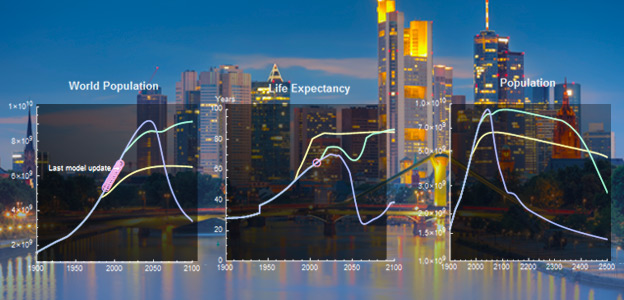See Example Modeling the World Combine system dynamics methodology with data from Wolfram|Alpha. See Example Other Use examples from a wide range of application areas to learn about modeling and simulation with SystemModeler and the Modelica language. Ice Pod Model ice contact with propellers and investigate these forces with standardized load test cases. 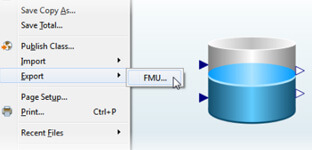See Example System Integration with FMI Use the Functional Mock-up Interface (FMI) to export a model from SystemModeler and import it in NI VeriStand to test a system in real time. See Example Electrical Circuit Reliability Use SystemModeler's reliability capabilities to study how heat affects the mean time to failure for an electrical circuit. See Example
