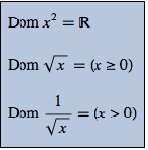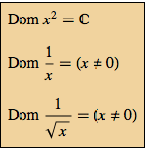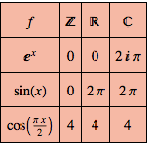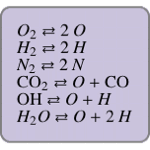4984

Enhanced Algebraic Computation

Enhanced Algebraic Computation in Mathematica 10

Mathematica Version 10 adds numerous extensions and improvements to its already strong capabilities in algebraic computation. Faster methods for symbolic solutions of real polynomial systems as well as numerical solutions of general polynomial systems make many problems computationally tractable for the first time. New, dedicated functions automate computing function domain, range, and periodicity. Finally, new matrix tests, enhanced matrix solvers, and many under-the-hood enhancements make linear algebra faster and easier than ever.

  • Support for computing the domain of a function over the reals, complexes, R^n, and C^n. »
  • Support for computing the range of a function into the reals, complexes, R^n, and C^n. »
  • Support for computing periodicity of functions over the integers, reals, and complexes. »
  • Fast symbolic solutions of real polynomial equations and inequalities using newly invented cylindrical decomposition method. »
  • Fast numeric solutions of real and complex polynomial equations based on algebraic homotopy computation. »
  • Full suite of matrix predicates, including tests for negative definite, Hermitian, orthogonal, and diagonalizable matrices. »
  • Matrix predicate support for numeric, exact, and symbolic matrices.
  • New and extended method support in solvers for linear equations, Riccati equations, and eigenvalue problems.
  • Updated base libraries for numerical linear algebra and high-precision arithmetic that support refined algorithms and modern computer architectures.

Real Function Domain Computation »
Complex Function Domain Computation »
Real Function Range Computation »
Complex Function Range Computation »

Real Function Period Computation »
Compare Periods over Different Domains »
Create a Function to Visualize Periodicity »
Functions with Multiple Periods »

Fast Symbolic Solving of Real Polynomial Systems »
High-Performance Numeric Solution of Polynomial Systems »
Solve Geometric Problems as Polynomial Systems »
Find Chemical Equilibrium for Networks of Reactions »

Matrix Predicates »
Symmetric Matrices »
Antisymmetric and Orthogonal Matrices »
Quantum Hamiltonian »