Finite-Elemente-Methode (FEM) als Kernbestandteil der Wolfram Language
Die Wolfram Language unterstützt sowohl Anfänger als auch Experten beim Erfassen des Verhaltens einer Konstruktion durch die Bereitstellung multiphysikalischer partieller Differentialgleichungsmodelle, Solver und nahtlos daran anknüpfende Post-Processing-Funktionen. Alle Elemente für FEM integrieren sich vollständing mit den fortschrittlichen Geometrie- und Visualisierungfunktionen der Wolfram Language.
Geometrische Modellierung
Geometrische Modellierung
Die Wolfram Language erlaubt es, präzise Simulationen zu entwerfen. Dazu werden geometrische Modelle aus mehreren Materialien mit booleschen Operationen oder impliziten Beschreibungen erstellt. Alternativ können die Modelle aus Punktdaten, Bildern, geografischen Karten o. ä. rekonstruiert werden. Des Weiteren können viele CAD- und andere Geometriedateiformate wie STEP, DXF und STL importiert werden.
Abgeleitete geometrische Regionen »
Monographie zum CAD-Interface »
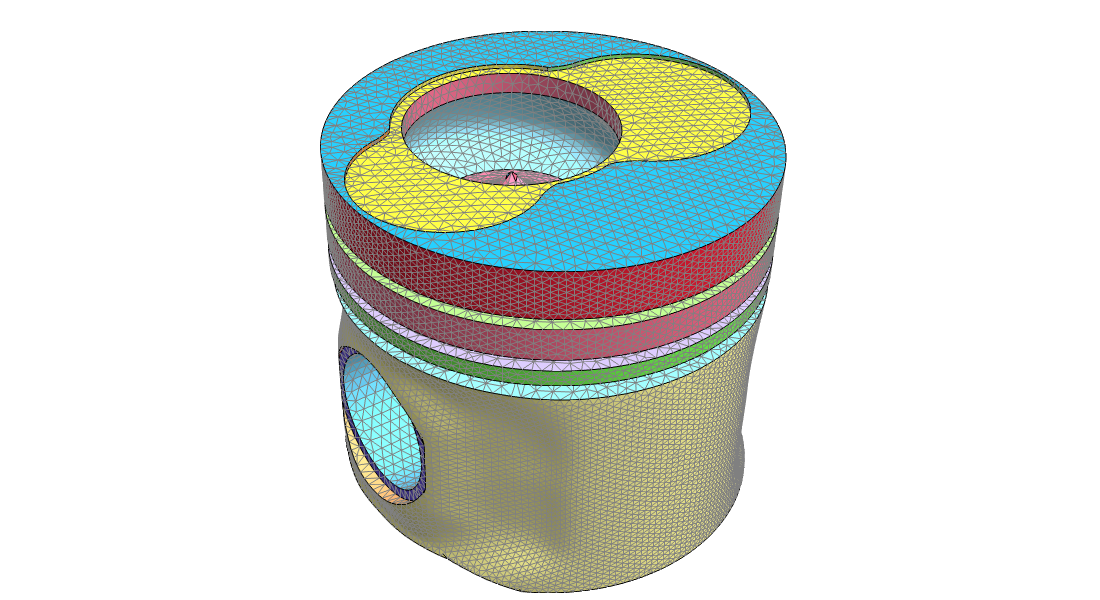
Gitternetze erzeugen
Gitternetze erzeugen
Für numerische Berechnungen, die mit der Wolfram Language durchgeführt werden, können Geometrien mit generierten oder importierten Meshes angenährt werden. Dabei können Verfeinerungen festgelegt, abgestufte oder gemappte Gitternetze erstellt und angepasste Schichten (Perfectly Matched Layer - PML) hinzugefügt werden, die zur jeweiligen Anwendung passen.
Monographie zur Erzeugung von Gitternetzten mit der FEM »
Monographie zur Visualisierung von Gitternetzen mit der FEM »
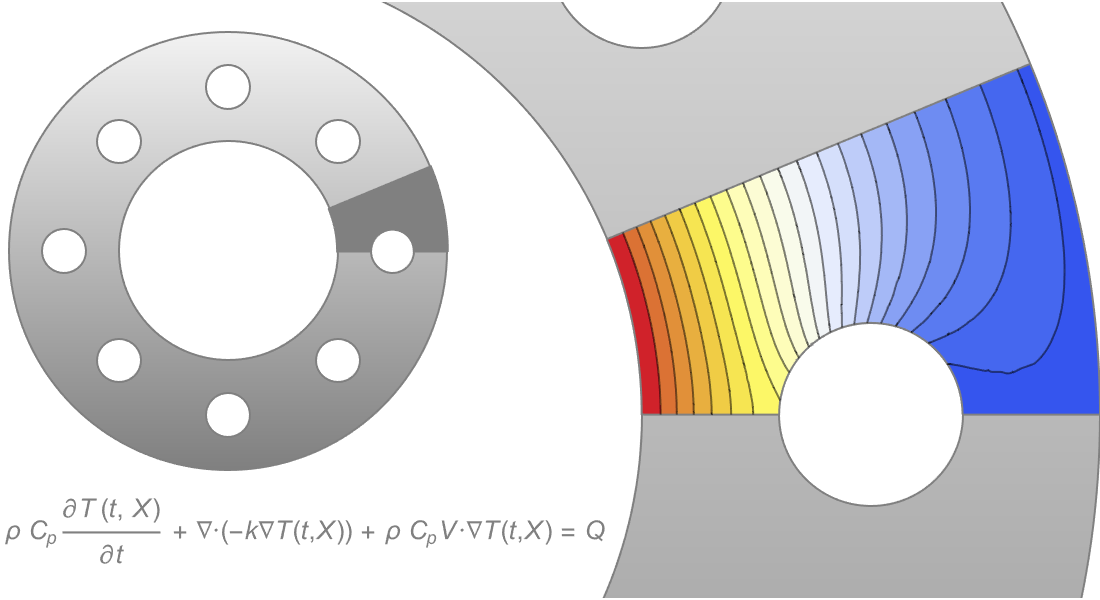
Wärmetransport
Wärmetransport
Mit der Wolfram Language lässt sich der Wärmetransport in multimateriellen, nichtlinearen, porösen, anisotropen Modellen mit Ereignissen oder Phasenänderungen in Flüssigkeiten oder Festkörpern berechnen. Es können unterschiedliche Randbedingungen, Perfectly Matched Layer (PML) und Quellenarten im ein-, zwei- oder dreidimensionalen Raum und für achsensymmetrische Fälle verwendet werden.
Leitfaden zur Modellierung von Wärmetransport mit partiellen Differentialgleichungen »
Monographie zum Wärmetransport »
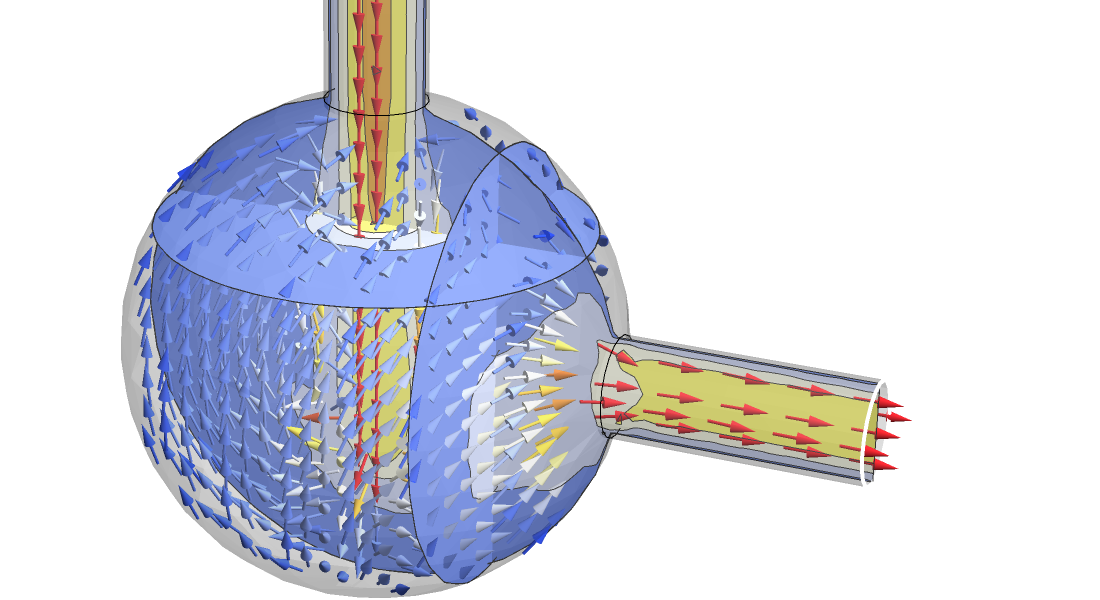
Fluiddynamik
Fluiddynamik
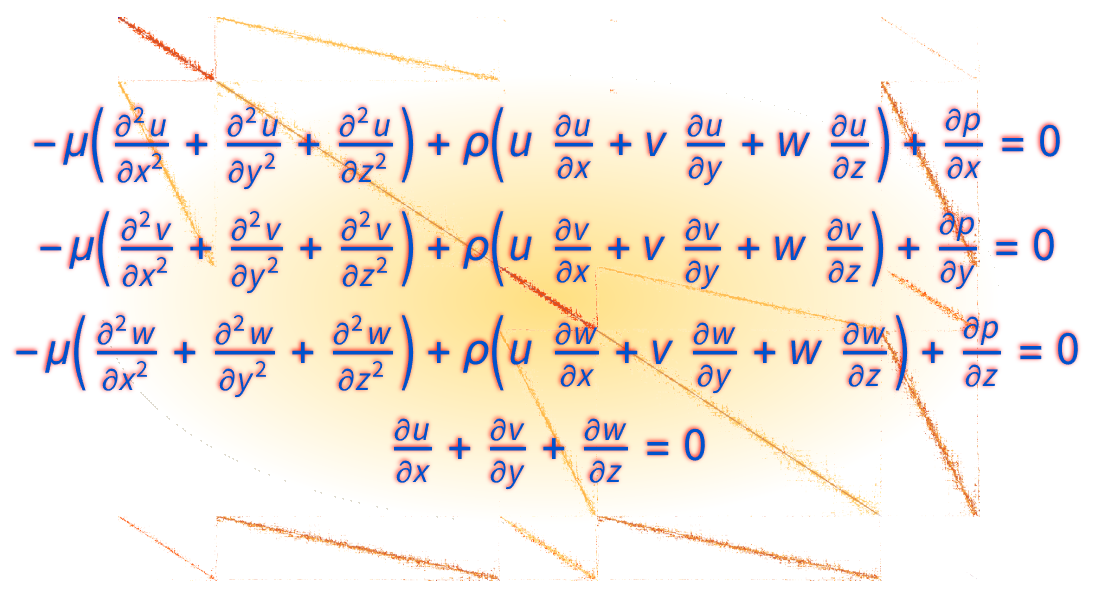
Neben der Analyse der Strömung von Flüssigkeiten können mit der Wolfram Language auch die Stokes- oder Navier-Stokes-Gleichungen in zwei oder drei Dimensionen gelöst werden. Auftriebsgetriebene Strömungen mit der Boussinesq-Näherung können modelliert oder die Navier-Stokes-Gleichung mit anderen Bereichen der Physik wie Wärmeübertragung oder Stofftransport gekoppelt werden.
Massetransport
Massetransport
Die Wolfram Language erlaubt die Modellierung von interphasigem oder anisotropem Stofftransport mit variablen, nichtlinearen Diffusionskoeffizienten einschließlich chemischer Reaktionen mit verschiedenen Quellen und Randbedingungen in einer, zwei oder drei Dimensionen sowie achsensymmetrischen Fällen.
Leitfaden für die Modellierung von Massetransport mit partiellen Differentialgleichungen »
Monographie zum Massetransport »
Leitfaden für Molekularstrukturen und Molekularinformatik »
Bildverarbeitung als Kernbestandteil der Wolfram Language »
Festkörpermechanik
Festkörpermechanik
Verschiebungen, Reaktionskräfte, Dehnungen sowie Spannungen können mittels der Wolfram Language berechnet werden. Ebenso stehen hyperelastische oder lineare und nichtlineare elastische, anisotrope Materialmodelle, eventuell gekoppelt mit Wärmeausdehung, zur Verwendung bereit. Auch können statische, zeitabhängige, parametrische sowie Frequenzgang-, Schwingungs- oder Eigenmoden-Analysen in 2D und 3D durchgeführt werden.
Leitfaden für die Modellierung von Festkörpermechanik mit partiellen Differentialgleichungen »
Monographie zur Mechanik fester Körper »
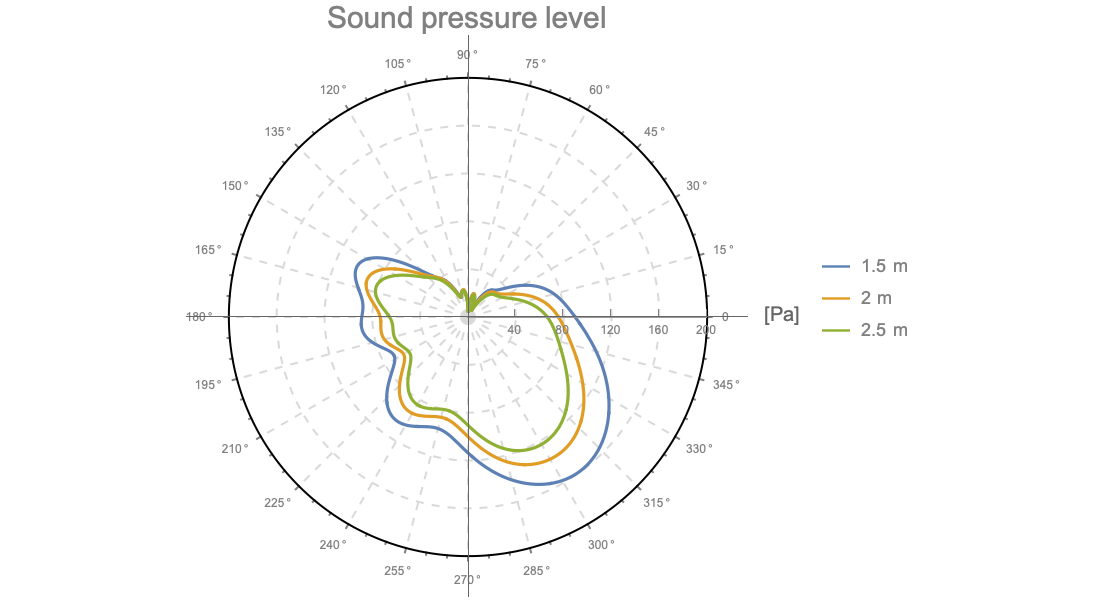
Akustik
Akustik
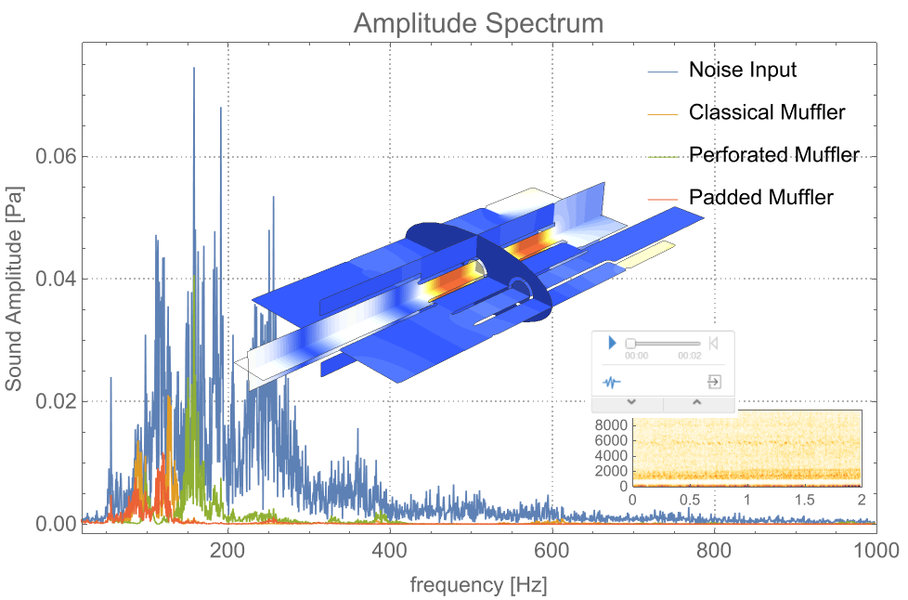
Die Wolfram Language bietet leistungsstarke Funktionen zur Modellierung von Multimaterial-Akustik im Zeit- oder Frequenzbereich. Weiterhin können harmonische oder Eigenfrequenzanalysen mit einer Vielzahl an Randbedingungen und Quellen durchgeführt werden. Genaue Lösungen werden durch die Verwendung von PMLs erreicht.
Leitfaden für die Akustikmodellierung mit partiellen Differentialgleichungen »
Monographie zur Akustik »
Leitfaden für Audioverarbeitung »
Multiphysikalische Systeme
Multiphysikalische Systeme
Physikalische Modelle lassen sich mit der Wolfram Language ohne zusätzliche Add-On-Pakete kombinieren. Anwendern eröffnen sich neue Möglichkeiten bei der Finite-Elemente-Analyse, indem sich die Analyse partieller Differentialgleichungen nahtlos mit dem Wolfram-Funktionen für Bildverarbeitung, Geografie, Chemie oder Signalverarbeitung kombinieren lässt. Modellkoeffizienten lassen sich aus Echtzeit-Sensordaten generieren oder aus kuratierten Daten zu einem breiten Themenspektrum beziehen.
Solver für Gleichungen
Solver für Gleichungen
Die Wolfram Language ermöglicht die Durchführung nichtlinearer, stationärer oder zeitanhängiger Analysen mit speziellen, vielseitigen iterativen und parallen, direkten oder Out-Of-Core-Solvern. Auch ein Eigenmode-SOlver und ein parametrischer Solver stehen bei Bedarf zur Verfügung. Dabei bestehen keine Beschränkungen in der Anzahl der verwendeten Knoten oder Elemente. Nichtlineare partielle Differentialgleichungen werden automatisch linearisiert.
Leitfaden für Solver über Regionen »
Leitfaden für Solver von Differentialgleichungen »
Integrierte Nachberarbeitung
Integrierte Nachbearbeitung
Mit der Wolfram Language ist auch die direkte Nachbearbeitung der Resultate möglich. In einer einzigen Arbeitsumgebung lassen sich qualitativ hochwertige Visualisierungen erstellen, mit berechneten Farbverläufen versehen oder gleich die Lösungen integrieren.
Leitfaden für die Funktionsvisualisierung »
Leitfaden für die Optimierung »
Leitfaden für den 3D-Druck »
Leitfaden für die Kurvenanpassung & Näherungsfunktionen »
FEM mit einer API programmieren
FEM mit einer API programmieren
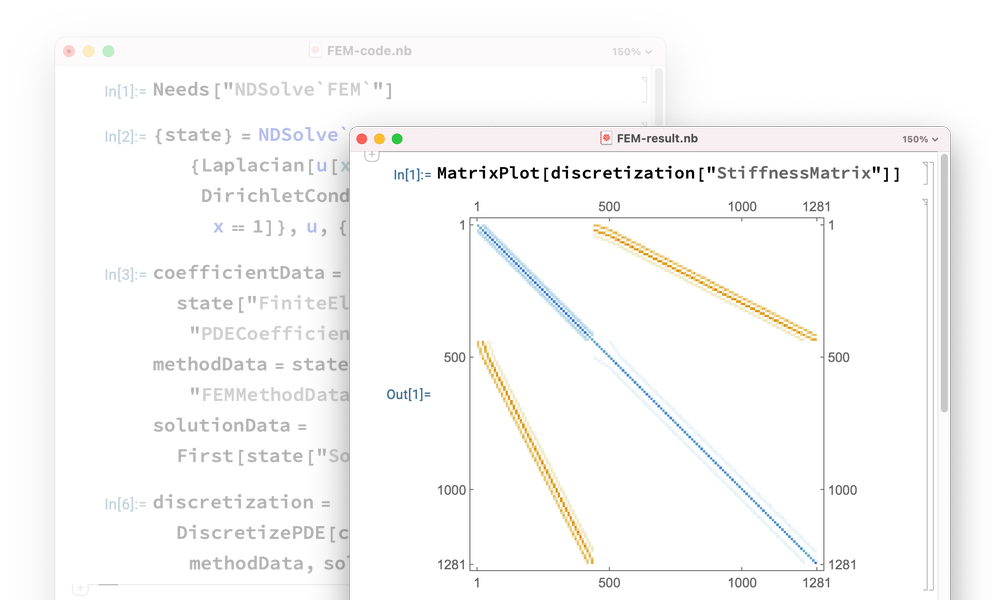
Jeder Aspekt des FEM-Lösungsprozesses kann mit der Wolfram Language in jeder Phase abgefangen und kontrolliert werden. Auch lassen sich neue Algorithmen für die Lösung von partiellen Differentialgleichungen entwickeln.
Monographie zum Programmieren mit der Finite-Elemente-Methode »
Wolfram Solutions
Nächste Schulungen
| Mathematica - Grundlagen und Programmiertechniken 02.02. - 05.02.2026 - Online |
| Modul: Einführung in Mathematica 13.04.2026 - Online |
| Modul: CDF-Programmierung mit Mathematica 13.04.2026 - Online |
Nächste Webinare
| Wolfram-Webinar: Power up your Plots 29.01.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Schnelleinstieg in die Wolfram Language und den System Modeler 19.02.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Neuronale Netze mit Mathematica - Konstruktion & Anwendung 05.03.2026 : 11:00 - 11:45 Uhr |
Buchen Sie Ihren Termin mit unseren Spezialisten
| Name | Produkt | Themen | |
|---|---|---|---|
 |
Harald Farcas | Wolfram Mathematica, Wolfram Finance Platform, System Modeler, Wolfram Cloud Produkte und Origin/OriginPro | Industrie, Behörden, akademische Kunden, Product Manager Wolfram, Schulungen und Produktvorstellung |
 |
Ralf Rosenberger | Origin/OriginPro, Mathematica, Minitab | Produktapplikation, professioneller Service, Beratung, Rahmenvereinbarungen |
 |
Andreas Heilemann | Mathematica, Minitab, OriginPro | Enterprise Business, Großkunden, Senior Key-Account-Manager |