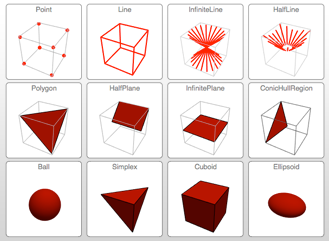
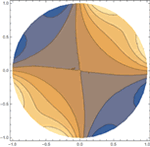
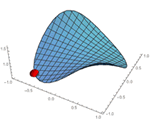
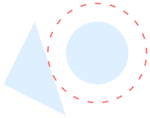
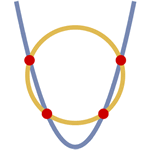
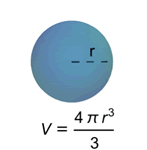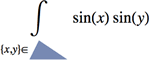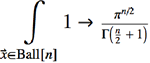Basic and Formula Regions
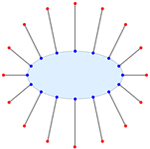
Mathematica Version 10 adds full support for basic and formula-based geometric regions. Basic regions are common and easy to specify. Formula regions are flexible and have great descriptive power. Basic and formula regions can be used to compute exact or approximate solutions or results involving parameters, often in any number of dimensions. Basic and formula regions fully support the geometric region framework, including computing properties (area, nearest point, etc.), being used as input to solvers (optimization, solving PDEs, etc.), and discretization.
|
|