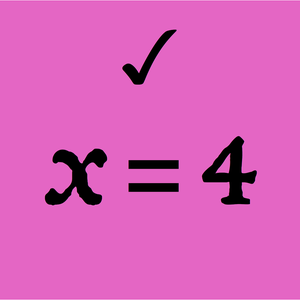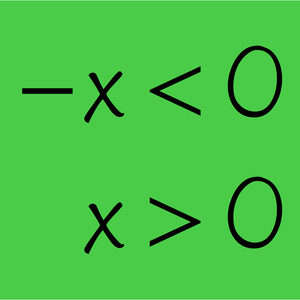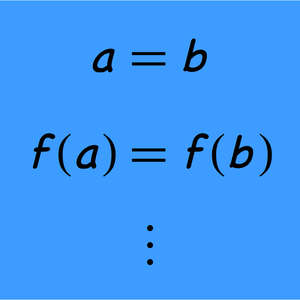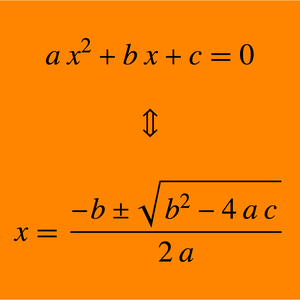Algebraic Computation
Version 12 of the Wolfram Language extends its already strong capabilities in algebraic computation with functionality for users ranging from pre-college students to researchers. Improvements span from new functions that manipulate equations step by step to more powerful equation and optimization solvers to equational theorem proving.
- Compute the boundary, connected components and other topological properties of solution sets for real polynomial systems. »
- Express large systems naturally and succinctly using vector and matrix variables. »
- Efficiently solve large systems of equations and inequalities with special structure. »
- Solve previously intractable classes of equation and inequality systems. »
- Formulate optimization problems in a more concise and natural way using vector and matrix variables. »
- Solve new classes of exact optimization problems. »
- Solve equations "step by step" using new functions to add, multiply and otherwise combine equations and inequalities. »
- Produce automatic proofs of equational logic theorems. »
- Prove theorems using a built-in collection of axiomatic theories. »
- Present proofs in various formats, including graphs, datasets and notebooks. »