Minitab 22 - Identifikation der Verteilung - Transformationen für Ryan-Joiner-Tests
- Erstellt am 23.5.2025
- Software: Minitab 22
 Das entsprechende APS-Paket ist über unseren ADDITIVE Professional Service erhältlich. Um das Paket zu erhalten, kontaktieren Sie unseren Support per E-Mail an
Das entsprechende APS-Paket ist über unseren ADDITIVE Professional Service erhältlich. Um das Paket zu erhalten, kontaktieren Sie unseren Support per E-Mail an
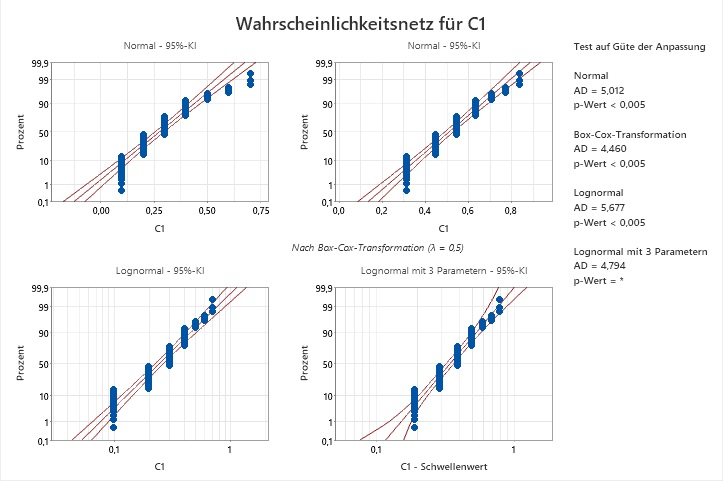
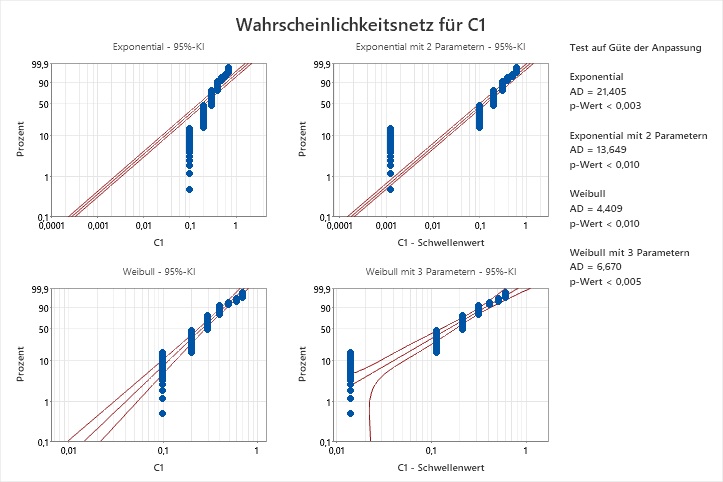
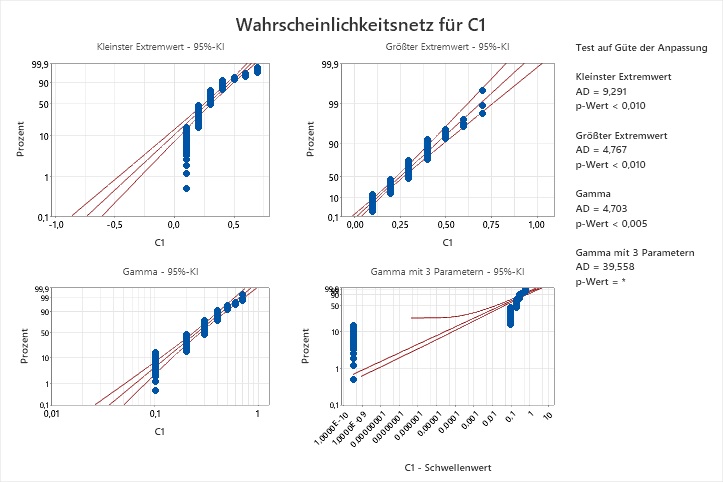
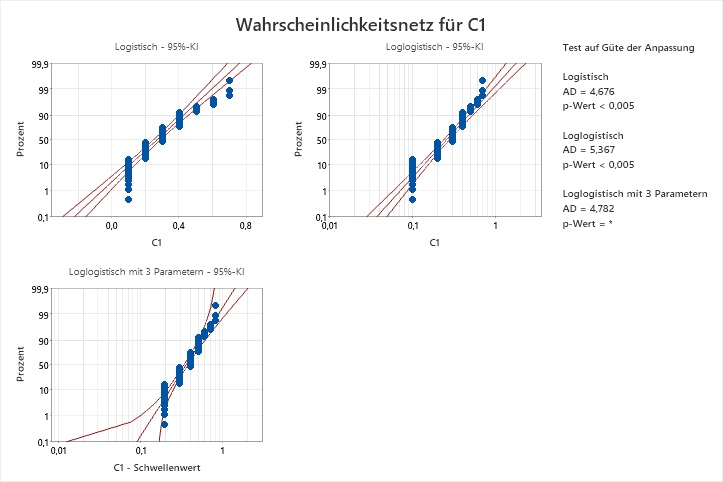
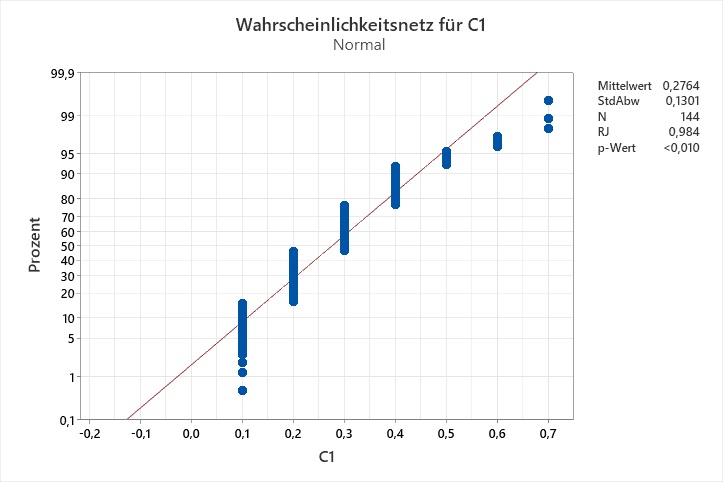
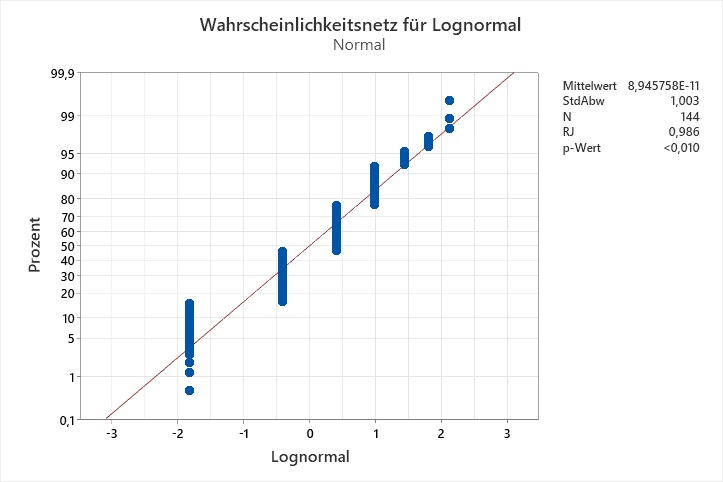
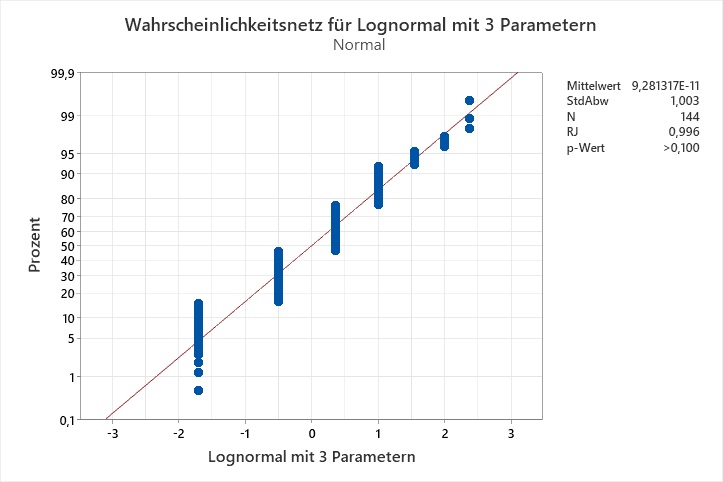
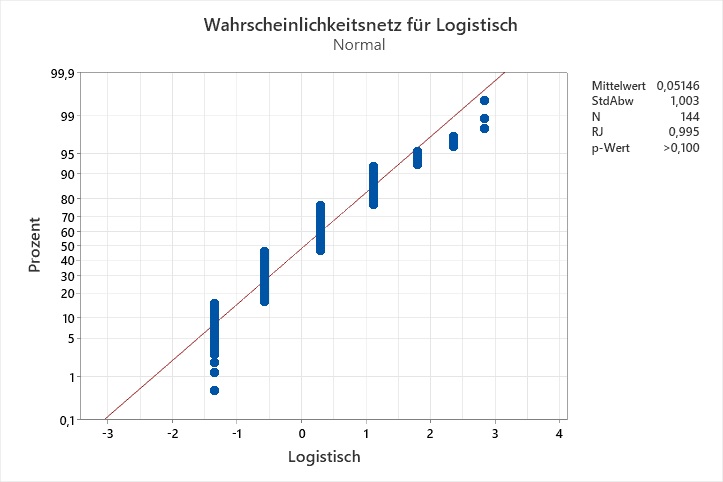
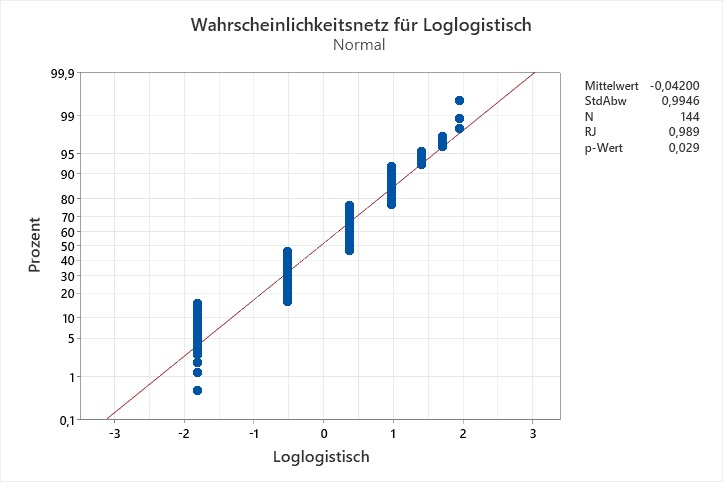
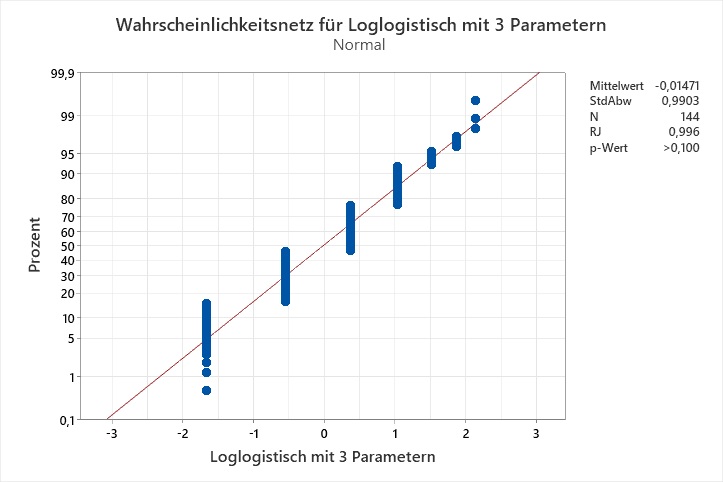
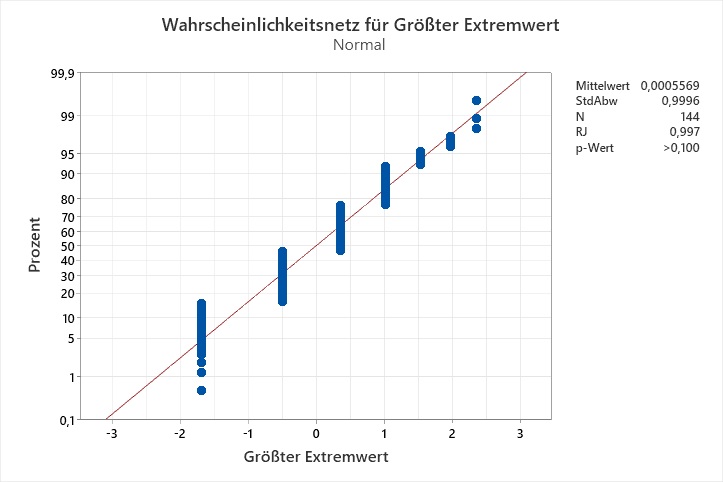
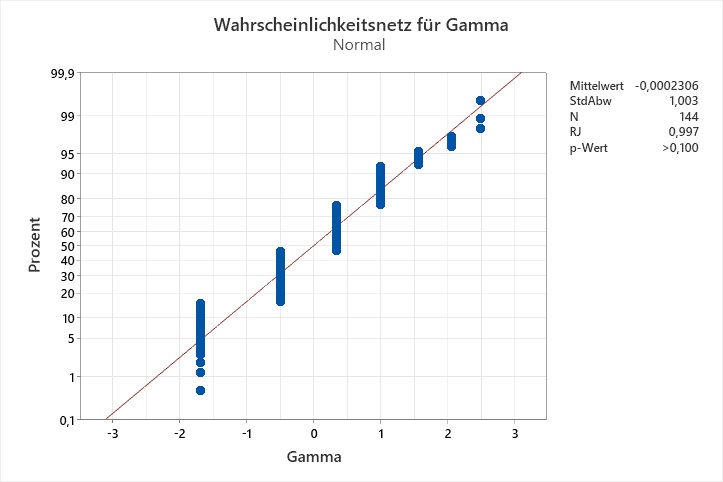
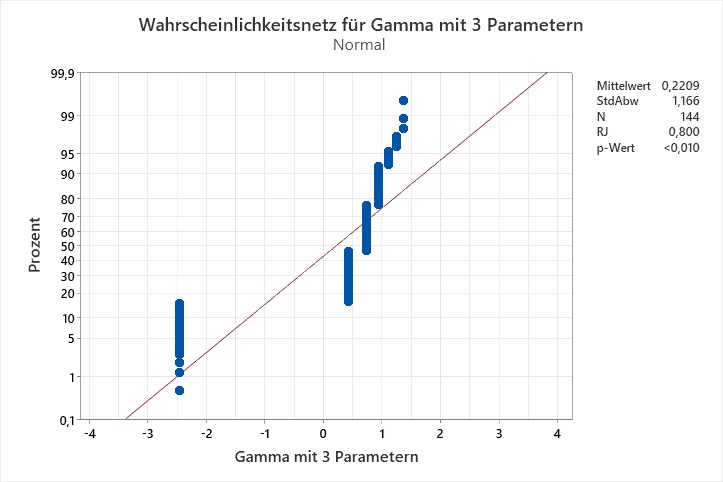
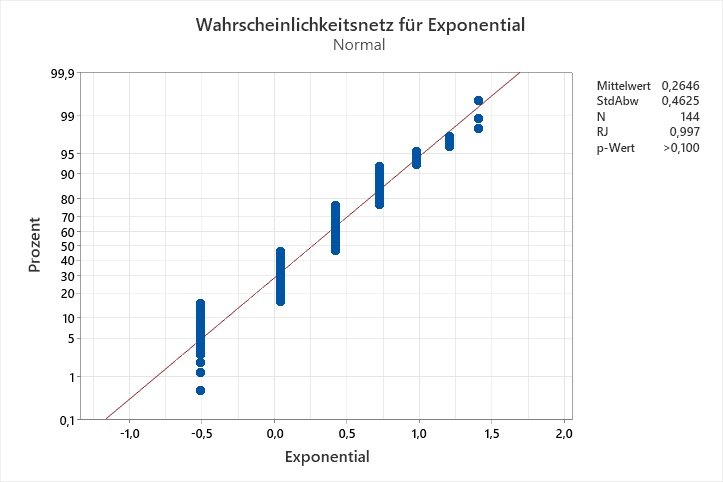
Ich habe eine Identifikation der Verteilung gemacht, und keine der Verteilungen passt laut den Anderson-Darling-Tests auf meine Daten. Die Wahrscheinlichkeitsnetze legen nahe, dass die Auflösung der Daten das Problem sein könnte:
Identifikation der Verteilung für C1
* HINWEIS * Fehler beim Auswählen einer Johnson-Transformationsfunktion mit p-Wert > 0,1. Es
wird keine Transformation ausgeführt.
Exponential mit 2 Parametern
* WARNUNG * Varianz-/Kovarianzmatrix von geschätzten Parametern ist nicht vorhanden. Der
Schwellenwertparameter wird als fest angenommen, wenn Konfidenzintervalle berechnet werden.
Gamma mit 3 Parametern
* WARNUNG * Varianz-/Kovarianzmatrix von geschätzten Parametern ist nicht vorhanden. Der
Schwellenwertparameter wird als fest angenommen, wenn Konfidenzintervalle berechnet werden.
Wie könnte ich mir in diesem Fall Abhilfe schaffen?
Erläuterung
Der Ryan-Joiner-Test auf Normalverteilung ist geeignet für Daten aus einer normalverteilten Grundgesamtheit, die eine geringen Auflösung besitzen. Jedoch ist ein Datensatz nicht immer aus einer normalverteilten Grundgesamtheit entnommen. Gemäß der Inversionsmethode könnte man die Daten von einer theoretischen Verteilung auf eine Normalverteilung transformieren. Die Idee ist: Wenn die Grundgesamtheit der theoretischen Verteilung folgt, folgen die transformierten Daten der Normalverteilung. Das APS-Paket Nr. ist ein Makro, das solche Transformationen für die Verteilungen Weibull, Weibull mit 3 Parametern, Kleinster Extremwert, Lognormal, Lognormal mit 3 Parametern, Logistisch, Loglogistisch, Loglogistisch mit 3 Parametern, Größter Extremwert, Gamma, Gamma mit 3 Parametern, Exponential und Exponential mit 2 Parametern durchführt und sowohl für die Originaldaten als auch für die transformierten Daten Ryan-Joiner-Tests durchführt.
Bitte legen Sie das Makro in dem Verzeichnis ab, dass Sie in Minitab unter Datei: Optionen als Speicherort für Makros festgelegt haben.
Beispiel
Die Daten sind in Spalte C1 hinterlegt. Der Befehl für den Aufruf des Makros ist
%ADD_sup_Verteilungsidentifikation_Transformation_Ryan_Joiner C1
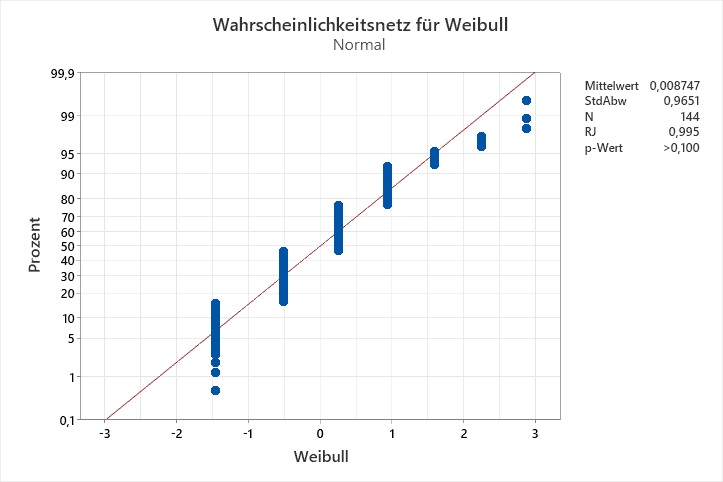
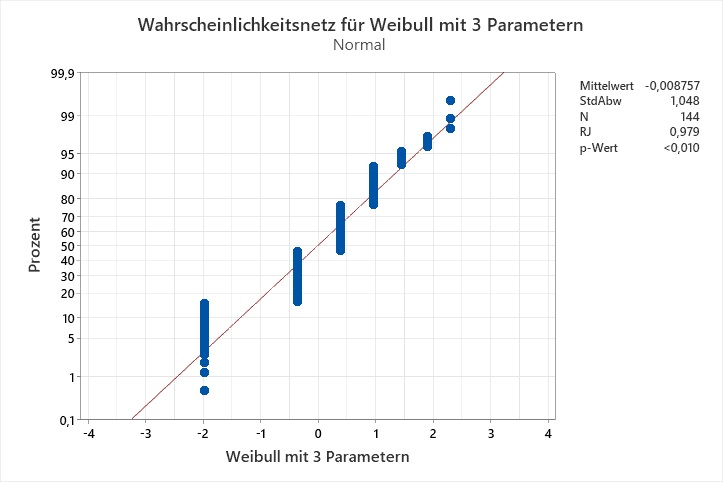
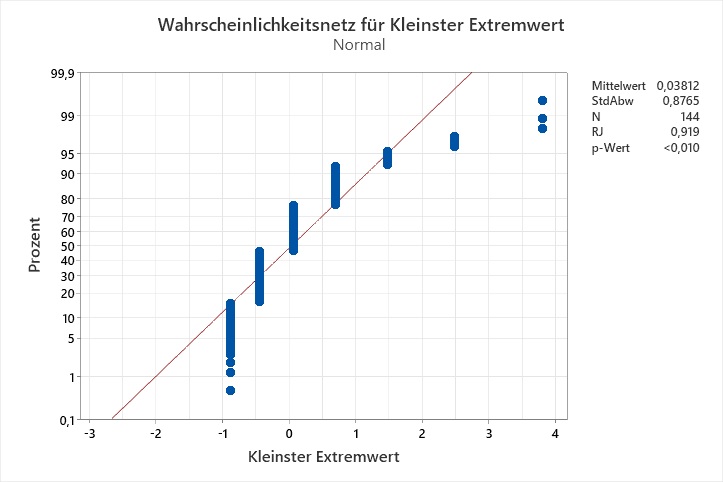
Ryan-Joiner-Tests für die Transformationen von C1
* WARNUNG * Varianz-/Kovarianzmatrix von geschätzten Parametern ist nicht vorhanden. Der
Schwellenwertparameter wird als fest angenommen, wenn Konfidenzintervalle berechnet werden.
Dieses Makro ist ein Beispiel für die Automatisierungsmöglichkeiten für Minitab. Trotz aller Sorgfalt übernehmen wir keine Gewährleistung für die Richtigkeit der Berechnungen und Ergebnisse.
|
|