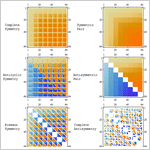
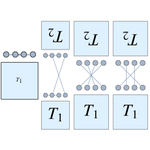
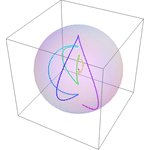
Eingebaute symbolische Tensoren

Mathematica 9 stellt nun die Unterstützung für symbolische Arrayobjekte von einfachen Vektoren bis hin zu jeglicher Dimensionalität und  Symmetrie vor. Neue Tensoralgebra- Operationen ermöglichen nun die Konstruktion von Polynomen symbolischer Arrays. Diese können nun durch effiziente Algorithmen in die Standardform vereinfacht werden. Ein neuer Typ von strukturierten Arrays speichert lediglich symmetrische und unabhängige Komponenten. Dieser ist Grundlage für einen effektiven Gebrauch des Speichers vor allem im Bereich von Antisymmetrien. Neue Differentialoperatoren für die Vektoranalyse können explizite Arrays eines unbestimmten Typs und Rangs behandeln und diese in verschiedenen orthogonalen Koordinatensystemen interpretieren.

• Symbolische Ausdrücke können Arrays jeglicher Dimension und Symmetrie repräsentieren
• Tensoralgebra- operationen beinhalten Tensorprodukte und mehr
• Modernste Kanonisierung von Tensorpolynomen
• Neuer Typ von Array der durch seine Symmetrie und unabhängigen Komponenten spezifiziert wird
• Differentialoperatoren wie Gradienten, Divergenz, Curl und Laplacian können auf Vektoren und Arrays jeglicher Dimension angewandt werden
• Neue kuratierte Daten von orthogonalen Koordinatensystemen können durch derivative Operatoren benutzt werden