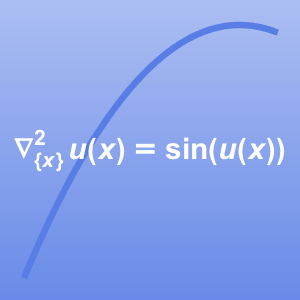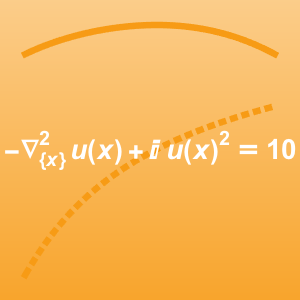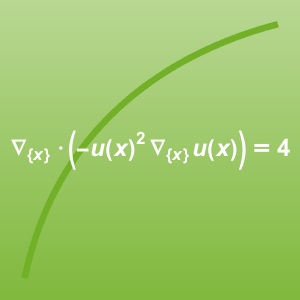Nonlinear Finite Elements
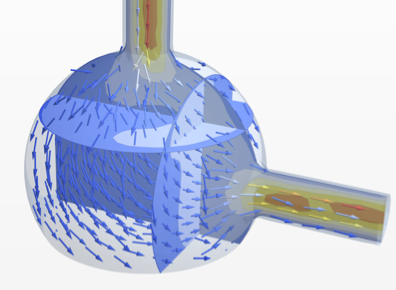
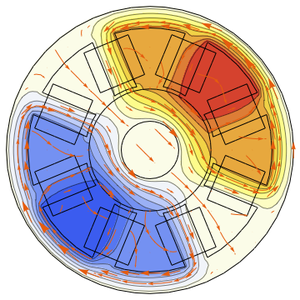
Version 12 extends its numerical partial differential equation-solving capabilities to solve nonlinear partial differential equations over arbitrary-shaped regions with the finite element method. Given a nonlinear, possibly coupled partial differential equation (PDE), a region specification and boundary conditions, the numerical PDE-solving capabilities find solutions to stationary and time-dependent nonlinear partial differential equations. This functionality will enable you to model a much larger class of industry-relevant applications from domains like physics, chemistry, mechanics, fluid dynamics and many more.
- Support for stationary nonlinear PDEs over regions. »
- Model with PDEs depending on space, time and the dependent. »
- Use PDEs depending on the derivative of the dependent. »
- Solve complex-valued nonlinear PDEs. »
- Specify nonlinear generalized Neumann boundary conditions. »
- Solve time-dependent nonlinear PDEs over regions. »