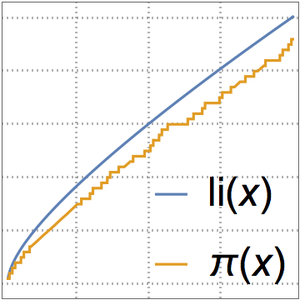
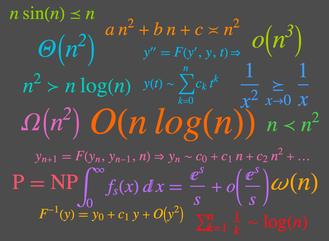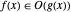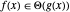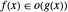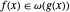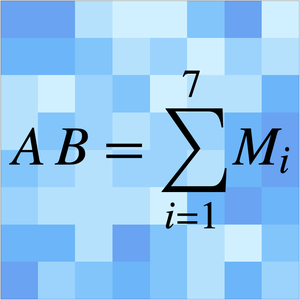Asymptotics
Asymptotic methods represent a third mode of computing that complements exact symbolic and approximate numeric modes of computing for calculus and algebra. Asymptotic methods are what disciplines turn to when they run into hard problems and are used in a wide variety of areas, including number theory, analysis of algorithms, statistics, theoretical physics and numerical methods. Asymptotic computing allows hard problems to be solved and furthermore is typically more insightful even when other modes of computing succeed. With Version 12, asymptotic computing is fully automated and as easy to use as other high-level solvers.