5065

Random Matrices

Random Matrices in Mathematica 11

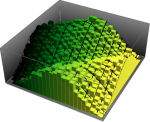
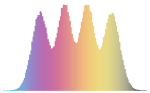
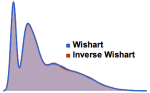
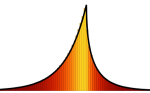
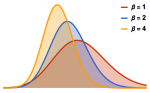
Mathematica Version 11 introduces support for random matrices. The efficient generation of matrix variates, estimation of their properties, and computations of their limiting distributions are tightly integrated with the existing probability & statistics framework. Random matrices have uses in a surprising variety of fields, including statistics, physics, pure mathematics, biology, and finance, among others.

Key Features

  • Efficient sampling from matrix distributions and their derived properties.
  • Support for Gaussian ensembles (GOE, GUE, ...).
  • Support for circular ensembles (COE, CUE, ...).
  • Support for Wishart and inverse Wishart distributions.
  • Support for matrix normal and distributions.
  • Support for limiting distributions of eigenvalues from matrix distributions, which include Wigner semicircle, Tracy–Widom, and Marchenko–Pastur distributions.
  • Numerical expectation computation of arbitrary matrix properties. »

Related Examples


Circular Ensembles (COE, CUE, ...) »
Gaussian Ensembles (GOE, GUE, ...) »
Wishart and Inverse Wishart Distributions »
Matrix Normal and Matrix T Distributions »

Properties of Matrix Distributions »
Eigenvalue Spacings of Gaussian Distributions »
Brownian Motion on CUE »
Dyson Coulomb Gas  »

Spectral Density of a Matrix »
Marchenko–Pastur Distribution »
Tracy–Widom Distribution »
Longest Increasing Subsequences »

Portfolio Correlation »
Random Rotations »
Simulate a Vector AR Process »
Zeros of the Riemann Zeta Function »