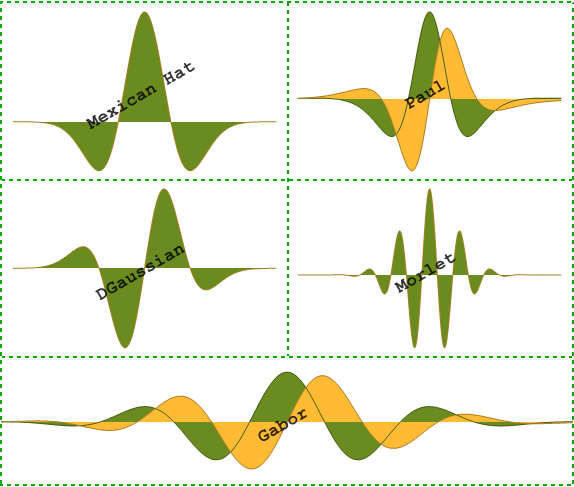
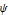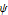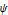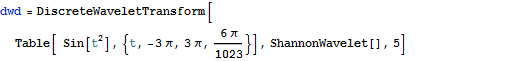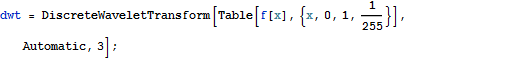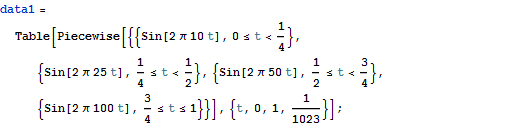Wavelet Analysis
With Mathematica 8, a complete system of wavelet methods is introduced in Mathematica.
Use discrete or continuous high-performance wavelet analyses for thresholding and visualization in any number of dimensions.
- Represention of many new discrete wavelet functions
- Represention of many new continuous wavelet functions
- Signal and image analysis
The user can transform his data in multiple wavelet bases, wavelet packet bases, or trigonometic bases, and perform inverse transforms in one or two dimensions. After that, the transform can be represented in a time-frequency space, and several different bases. Also, boundary values can be selected. Compressing and denoising of data prove to be surprisingly simple processes, which can be performed by using the integrated functions of the wavelet collection.
Zeitkontinuierliche Wavelet-Transformation
Diskrete Wavelet Familien
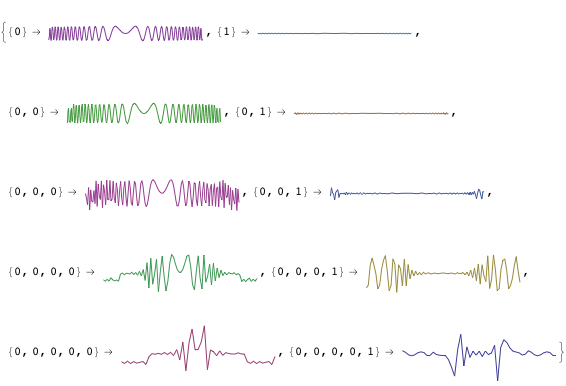
Discrete Wavelet Families
Show the scaling function ( ) and wavelet function (
) and wavelet function (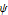 ) for several discrete wavelet families.
) for several discrete wavelet families.
Eigenschaften von Wavelet Familien
Get Properties for Wavelet Families
Directly get the scaling function ( ), wavelet function (
), wavelet function ( ), and filter coefficients for each wavelet family, or use them to specify a wavelet transform.
), and filter coefficients for each wavelet family, or use them to specify a wavelet transform.
To show Mathematica code, please click "plus".

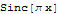

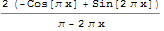
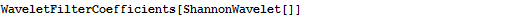

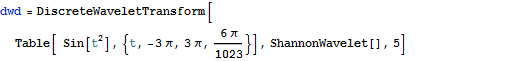

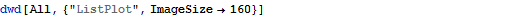
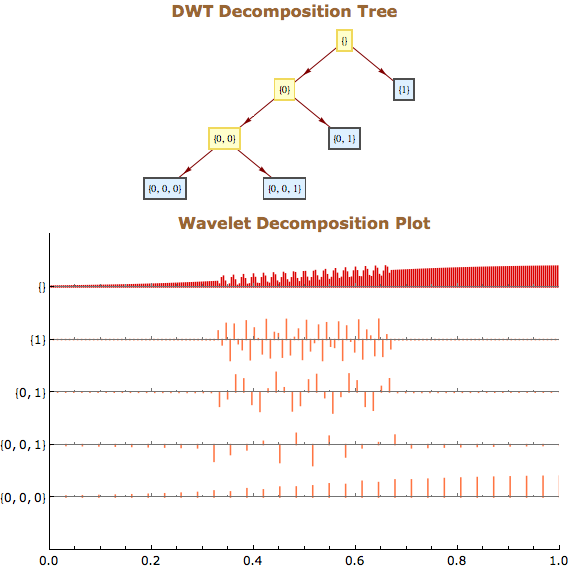
Diskrete Wavelet Transformation
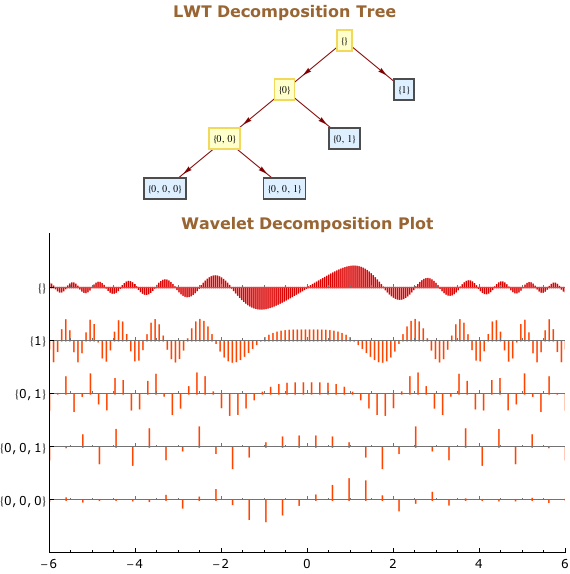
Lifting Wavelet Transformation
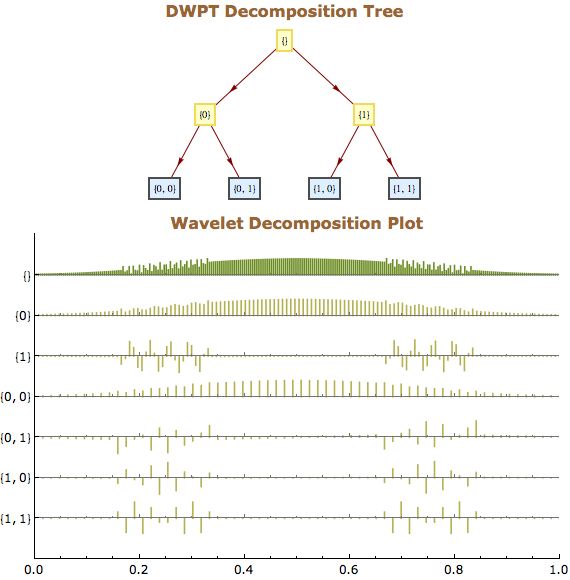
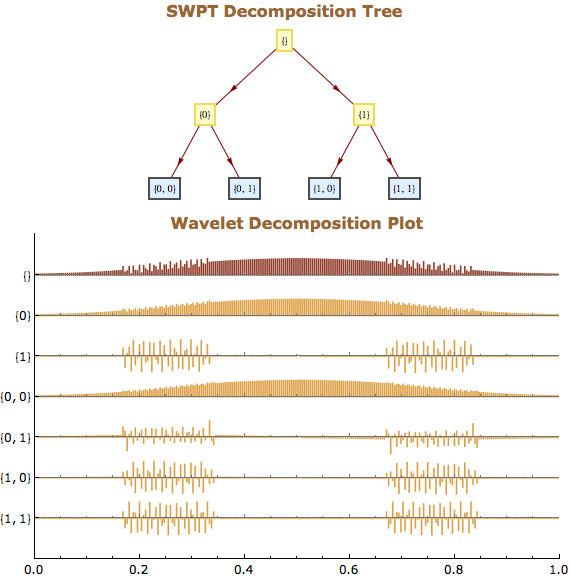
Diskrete Wavelet Paket Transformation
Stationäre Wavelet Paket Transformation
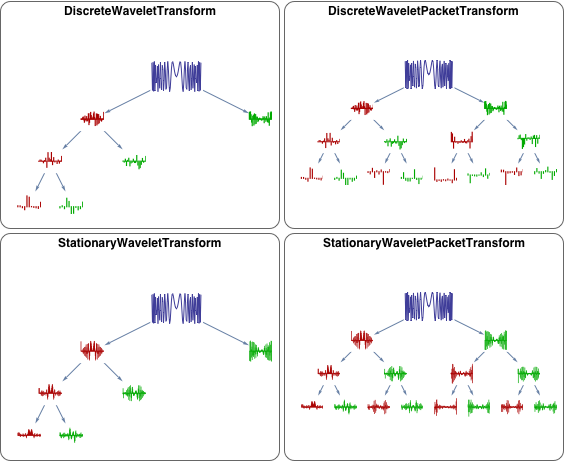
Unterschiede der DWT
Compare Discrete Wavelet Transforms
Transformieren von Bildern
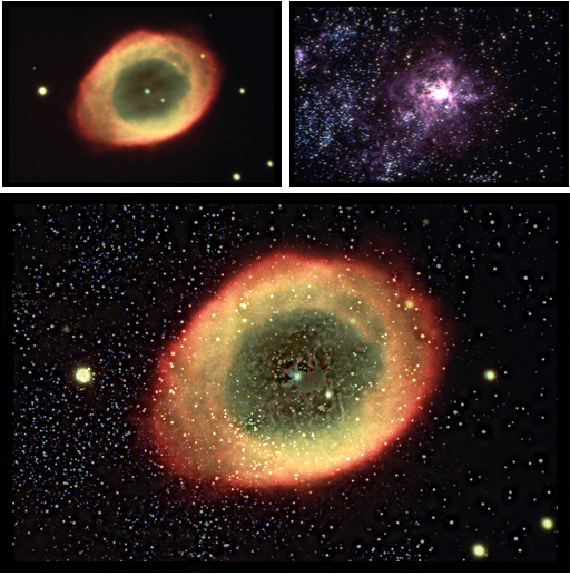
Überlagerung von zwei Bildern
Wavelet Image Fusion
Blend two images.
To show Mathematica code, please click "plus".




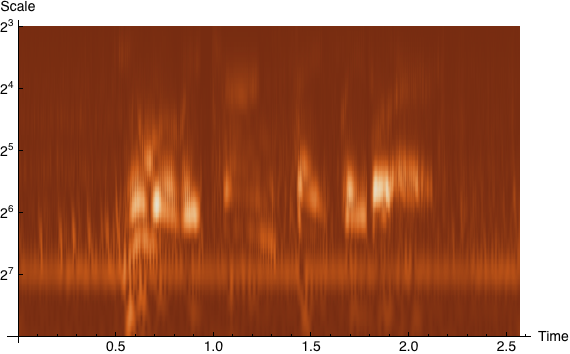
Visualisieren eines Scalogramms
Visualize Scalograms
To show Mathematica code, please click "plus".
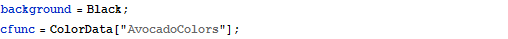
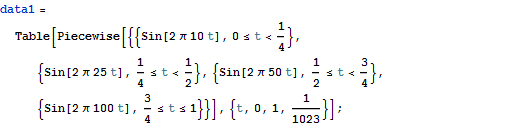



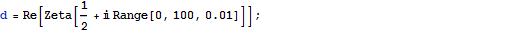
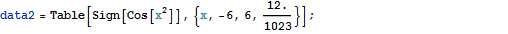
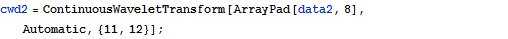


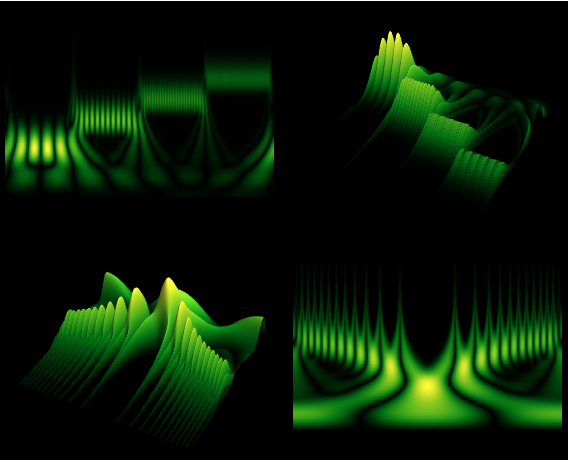
Transformieren von Geräuschen