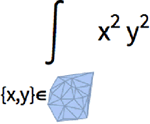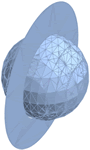
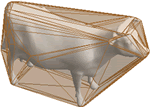
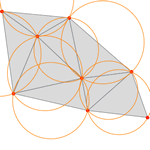
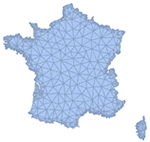
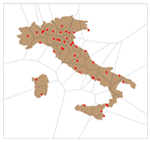
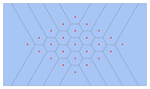
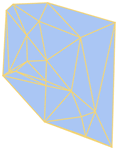
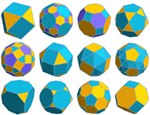
Data and Mesh Regions Mathematica Version 10 adds full support for mesh-based geometric regions. Mesh-based regions can be explicitly specified or automatically generated from lists of points, from graphics, or from other regions. Mesh-based regions are flexible enough to approximate any other region and support fast algorithms for essentially any operation. The mesh-based regions fully support the geometric region framework, including computing properties (area, nearest point, etc.) and being used as inputs to solvers (integration, solving PDEs, etc.). Full support for meshes in 1D, 2D, and 3D. » Ability to represent low-dimensional regions, e.g. curves in 2D, surfaces in 3D. Ability to represent non-manifold regions. Full support for boundary representation meshes in 1D, 2D, and 3D. » Ability to represent holes in 2D, as well as voids and tunnels in 3D. High-level support for styling and labeling of mesh cells. » Mesh generation from point sets, including Delaunay, Voronoi, and convex hull. Support for mesh triangulation with high-level controls. » Automatic discretization of 2D and 3D graphics. » Automatic discretization of any region. » Full support for computing key region properties such as membership test, distance computation, nearest points, measure (length, area, volume), centroids, etc. » Integrate over mesh-based regions. » Solve partial differential equations over mesh-based regions. » Support for low-level programming operations involving cells and coordinates. Support for cell-level properties, for instance, to store material or other properties. Meshes in 1D » Meshes in 2D » Meshes in 3D » Mixed-Dimension Meshes » Convex Hulls » Delaunay Meshes » Triangulating Meshes » Discretizing Regions » Discretizing Graphics » Create a Mesh Region from Image Data » Create a Mesh Region from Geographic Data » Create a Mesh Region from Lattice Points » Highlight Mesh Components » Label Mesh Components » Styling Mesh Components » Visualize Mesh Properties » Measures » Computing Distances and Nearest Points » Testing Membership » Computing Bounds » Integrating over a Mesh » Computing a Region's Moment of Inertia » Solving Differential Equations on a Mesh » Visualize PDE Solutions on a 3D Mesh »
