Stochastische Prozesse
Mathematica 9 bietet breite Unterstützung für Zufallsprozesse, in denen Vorgänge modelliert werden, welche sich mit der Zeit nicht deterministisch, sondern vielmehr zufällig entwickeln, aber in denen zeitlich folgende Zustände von einander abhängig sind. Zufallsprozesse, wie Verteilungen, sind symbolische Ausdrücke und können auf der Grundlage von Daten simuliert oder geschätzt werden. Der Wert eines Prozesses zu einem bestimmten Zeitpunkt ist wieder eine Verteilung und kann als solche in Mathematica verwendet werden.
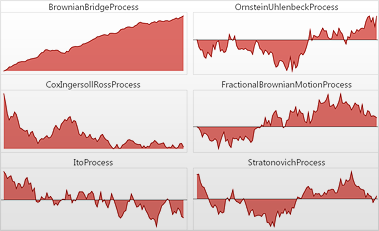
Mathematica 9 unterstützt eine große Anzahl an stochastischen Prozessen wie Parametrische Prozesse, finite Markov-Prozesse, Queueing Prozesse, Zeitreihenprozesse und Prozesse stochastischer Differentialgleichungen.
- Direktes Simulieren einer oder mehrerer Pfade für jeden Prozess
- Einfaches Arbeiten mit regulären und irregulären, skalaren und vektoriellen, univariaten und multivariaten Zeitreihendaten
- Automatisches Schätzen geeigneter Prozess-Parameter aus den Zeitreihendaten
- Arbeiten mit Verteilungen aus einfachen oder multiplen Zeitintervallen
- Direktes Berechnen statistischer Kennzahlen wie Mittelwert, Median, Varianz, etc.
- Direktes Berechnen von Kovarianz, Korrelation und absoluter Korrelationsfunktionen
- Verwendung der Zufallsprozesse für die Berechnung von Wahrscheinlichkeiten und Erwartungswerten
- Volle Unterstützung für symbolische, numerische und statistische Methoden für Prozesse
- Volle Unterstützung für eine große Zahl von Parametrischen Zufallsprozessen
- Volle Unterstützung für diskrete und stetige finite Markov-Prozesse
- Volle Unterstützung für allgemeine Warteschlangenprozesse und Warteschlangennetze
- Volle Unterstützung für Zeitreihenprozesse
- Volle Unterstützung für Prozesse stochastischer Differentialgleichungen