6066
Details
Category: Minitab FAQ Analysen
There is no translation available.

Minitab 22 - Beispiel für eine stückweise Regression

  • Erstellt am 6.6.2018
  • Überarbeitet am 10.4.2024
  • Software: Minitab 22, 21, 20, 19, 18

In diesem Beispiel zeigen wir ein Beispiel für eine stückweise Regression auf zwei verschiedenen Intervallen.





↓
C1
C2








 
x
y








1
1
0,42620475403394747








2
1
-0,01515472162335077








3
1
0,41265845607806578








4
1
0,12537041157007758








5
1
0,11100290939463248








6
1
0,26413370661574481








7
1
-0,74081701344303197








8
1
-1,38535789571209490








9
1
-0,00395002057379260








10
1
1,63751302058367990








11
2
3,34265600711087260








12
2
-0,00952342500131875








13
2
1,50150213334024300








14
2
2,34927912578673310








15
2
2,43436743942352280








16
2
1,02644543428312400








17
2
2,51273856281566750








18
2
2,60233067807299710








19
2
0,85103863613106823








20
2
2,94350047762518810








21
3
6,00412670621721660








22
3
5,35736499289219110








23
3
3,81699972641321810








24
3
6,36565717611459370








25
3
5,54816840922314030








26
3
7,71740852774209070








27
3
7,71155224911434800








28
3
6,93258542705701860








29
3
5,89438715870226380








30
3
6,29787897205976320








31
4
11,74825717978280400








32
4
11,03140798235927300








33
4
13,08201559982456000








34
4
13,19244931407598100








35
4
12,55944015036232400








36
4
12,01229231997890800








37
4
11,99427137424747000








38
4
11,83993704875957300








39
4
11,54541079597726100








40
4
13,09899175819151500








41
5
19,23952591477400600








42
5
19,54548330350446200








43
5
18,47343462225741100








44
5
21,45582748264180100








45
5
20,61612927666164900








46
5
20,54683542331031300








47
5
19,39556059207658100








48
5
18,36135807775946200








49
5
18,75591076009471400








50
5
21,24961142081160400








51
6
3,43527452797019350








52
6
5,67660195317558450








53
6
4,54175389188676700








54
6
3,24534195142399890








55
6
5,91245365385224280








56
6
2,82492965944049960








57
6
4,35193041207642390








58
6
4,87634814183994790








59
6
5,02799143952945470








60
6
2,91122680434667910








61
7
3,17403974898428130








62
7
3,94650480932658350








63
7
2,62984613833009820








64
7
4,23107733152426850








65
7
3,76131916479595670








66
7
3,02276245171454510








67
7
4,86866854319095670








68
7
3,54544131880658140








69
7
2,49735635492597300








70
7
2,70904608332453730








71
8
1,20896034399591560








72
8
2,77785735450581580








73
8
1,83326863093898850








74
8
3,56176184935416980








75
8
1,24943236782380040








76
8
3,03412875538256800








77
8
1,33753233167663410








78
8
0,97537295743152086








79
8
1,43002634569296920








80
8
2,05493291893073860








81
9
0,44431185737368395








82
9
1,84029046881435220








83
9
1,48003415993487760








84
9
3,86520916883473120








85
9
0,77265865511493459








86
9
2,34926970597230420








87
9
1,83982270612668590








88
9
3,07092689766069070








89
9
1,34522973124257210








90
9
2,26103502594294880








91
10
0,16603686749374091








92
10
0,52110979858386841








93
10
-0,79071610768682987








94
10
1,92983021730639950








95
10
0,03925939670656575








96
10
0,87002449884333899








97
10
0,55205923677448254








98
10
0,68452433608685581








99
10
0,11561651363892622








100
10
-0,20655586957719763

 

Erläuterung

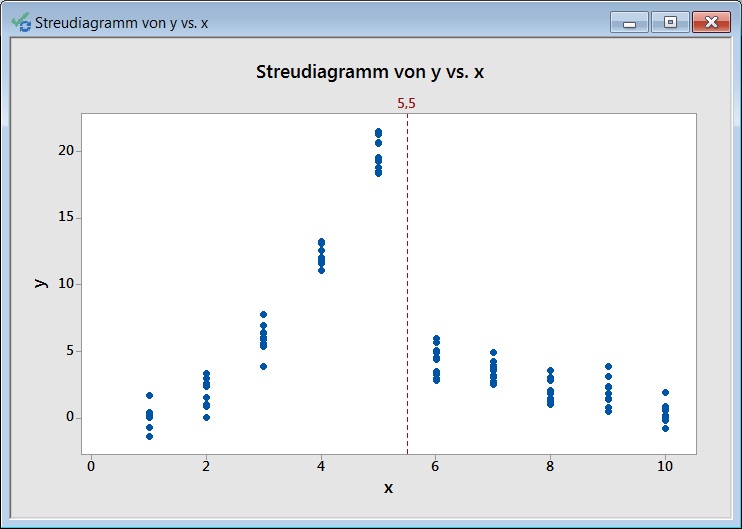
Wenn Sie diesen Datensatz mit einem Streudiagramm plotten (Grafik: Streudiagramm), sehen Sie, dass bei ungefähr 5,5 eine Grenze ist, in dem sich der funktionale Verlauf des Datensatzes ändert. Diese Grenze haben wir hier als Referenzlinie hinzugefügt:

beispiel_fuer_eine_stueckweise_regression_01

Mit der Rechnerfunktion

If(Test;Wert_wenn_wahr;[Wert_wenn_falsch])

macht das Programm einen Test, ob der Datensatz unterhalb der Grenze liegt:

'x' <= gr1

wobei gr1 = 5,5 ist.

Ein Ansatz über das Werkzeug  Statistik: Regression: Nichtlineare Regression wäre das Verwenden dieser Rechnerfunktion, um dem Programm zu sagen: Passe mir unterhalb dieser Grenze die Funktion

a0 + a1*'x' + a2*'x'^2

und oberhalb dieser Grenze die Funktion

b0 + b1*'x'

an.

In diesem Bildschirmvideo führen wir diesen Ansatz an einem Beispieldatensatz mit dem festen Wert gr1 = 5,5 und den Parameterstartwerten a0 = a1 = a2 = b0 = b1 = 1 durch.

Question?

This email address is being protected from spambots. You need JavaScript enabled to view it., wenn Sie eine Frage zu diesem Artikel haben.