Minitab 22 - Regression - Lineares/Polynomiales Modell versus Nichtlineare Regression - Zwei Beispiele
- Erstellt am 16.2.2023
- Überarbeitet am 9.4.2024
- Software: Minitab 22, 21
Bei linearen und polynomialen Modellen, deren Terme keine Abhängigkeiten oder zu hohe Multikollinearitäten aufweisen, konvergiert der Fit ohne Eingabe von Startwerten. Bei einem allgemeineren, nichtlinearen Modell konvergiert der Fit nicht immer, und es müssen Startwerte verwendet werden. In diesem Artikel verdeutlichen wir das an zwei Beispielen.
Erläuterung
Beispiel 1: Polynomiales Modell
Die Prädiktoren x und y und die Antwort z nehmen die folgenden Werte an:
| x |
y |
z |
| 1 | 1 | 6 |
| 1 | 1 | 8 |
| 1 | -1 | 1 |
| 1 | -1 | 1 |
| -1 | 1 | 2 |
| -1 | 1 | 0 |
| -1 | -1 | 3 |
| -1 | -1 | 4 |
Das Modell ist z=a+b*x+c*y+d*x*y+ε, wobei ε der Fehlerterm ist. Als Summe der kleinsten Fehlerquadrate ergibt sich
(a+bx1+cy1+dx1y1-z1)2+(a+bx2+cy2+dx2y2-z2)2+(a+bx3+cy3+dx3y3-z3)2+(a+bx4+cy4+dx4y4-z4)2+(a+bx5+cy5+dx5y5-z5)2+(a+bx6+cy6+dx6y6-z6)2+(a+bx7+cy7+dx7y7-z7)2+(a+bx8+cy8+dx8y8-z8)2
=(a+b+c+d-6)2+(a+b+c+d-8)2+(a+b-c-d-1)2+(a+b-c-d-1)2+(a-b+c-d-2)2+(a-b+c-d)2+(a-b-c+d-3)2+(a-b-c+d-4)2
Um die Summe der Fehlerquadrate zu minimieren, können wir die partiellen ersten Ableitungen nach den unbekannten Koeffizienten a, b, c, d, e und f bilden und die Werte für die Koeffizienten suchen, für die alle partiellen Gleichungen 0 werden. Dadurch erhalten wir das lineare Gleichungssystem
2(a+b+c+d-6)+2(a+b+c+d-8)+2(a+b-c-d-1)+2(a+b-c-d-1)+2(a-b+c-d-2)+2(a-b+c-d)+2(a-b-c+d-3)+2(a-b-c+d-4)=0
2(a+b+c+d-6)+2(a+b+c+d-8)+2(a+b-c-d-1)+2(a+b-c-d-1)-2(a-b+c-d-2)-2(a-b+c-d)-2(a-b-c+d-3)-2(a-b-c+d-4)=0
2(a+b+c+d-6)+2(a+b+c+d-8)-2(a+b-c-d-1)-2(a+b-c-d-1)+2(a-b+c-d-2)+2(a-b+c-d)-2(a-b-c+d-3)-2(a-b-c+d-4)=0
2(a+b+c+d-6)+2(a+b+c+d-8)-2(a+b-c-d-1)-2(a+b-c-d-1)-2(a-b+c-d-2)-2(a-b+c-d)+2(a-b-c+d-3)+2(a-b-c+d-4)=0
oder vereinfacht
16a-50=0
16b-14=0
16c-14=0
16d-34=0
was eine angepasste Funktion z=258+78*x+78*y+178*x*y+ε, wobei ε ergeben würde. Wir halten hier fest, dass wir das Ergebnis aufgrund des vollen Rangs der Designmatrix und keiner zu hohen Multikollinearitäten eindeutig lösen konnten.
Beispiel 2: Nichtlineares Modell
Der Prädiktor x und die Antwort y nehmen die folgenden Werte an:
| x |
y |
| 1 | 0,7804 |
| 2 | 0,7739 |
| 3 | 0,7667 |
| 4 | 0,7588 |
| 5 | 0,7500 |
Das Modell ist y=Sin(Exp(-λ*Exp(λ*x))), wobei ε der Fehlerterm ist. Als Summe der kleinsten Fehlerquadrate ergibt sich
(Sin(Exp(-λ*Exp(λ*x1)))-y1)2+(Sin(Exp(-λ*Exp(λ*x2)))-y2)2+(Sin(Exp(-λ*Exp(λ*x3)))-y3)2+(Sin(Exp(-λ*Exp(λ*x4)))-y4)2+(Sin(Exp(-λ*Exp(λ*x5)))-y5)2
=(Sin(Exp(-λ*Exp(λ*1)))-0,7804)2+(Sin(Exp(-λ*Exp(λ*2)))-0,7739)2+(Sin(Exp(-λ*Exp(λ*3)))-0,7667)2+(Sin(Exp(-λ*Exp(λ*4)))-0,7588)2+(Sin(Exp(-λ*Exp(λ*5)))-0,75)2
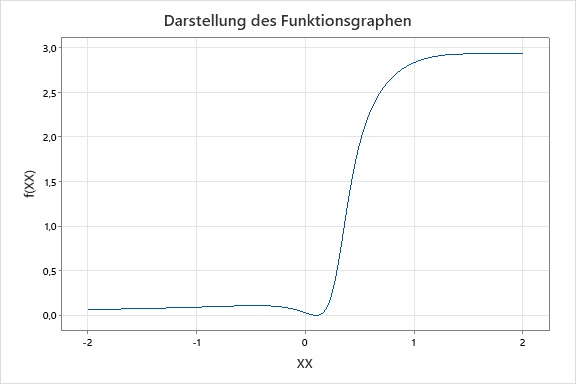
Wenn wir den Funktionsgraphen der Summe der kleinsten Quadrate für den Parameter λ darstellen, sehen wir, dass es ein lokales Minimum zwischen 0 und 1 zu geben scheint.
Wir könnten also die erste Ableitung der Summe der Quadrate bilden und eine Nullstelle zwischen 0 und 1 suchen:
2(-λexp(λ)-exp(λ))exp(-λexp(λ))(sin(exp(-λexp(λ)))-0,7804)cos(exp(-λexp(λ)))+2(-2λexp(2λ)-exp(2λ))exp(-λexp(2λ))(sin(exp(-λexp(2λ)))-0,7739)cos(exp(-λexp(2λ)))+2(-3λexp(3λ)-exp(3λ))exp(-λexp(3λ))(sin(exp(-λexp(3λ)))-0,7667)cos(exp(-λexp(3λ)))+2(-4λexp(4λ)-exp(4λ))exp(-λexp(4λ))(sin(exp(-λexp(4λ)))-0,7588)cos(exp(-λexp(4λ)))+2(-5λexp(5λ)-exp(5λ))exp(-λexp(5λ))(sin(exp(-λexp(5λ)))-0,75)cos(exp(-λexp(5λ)))
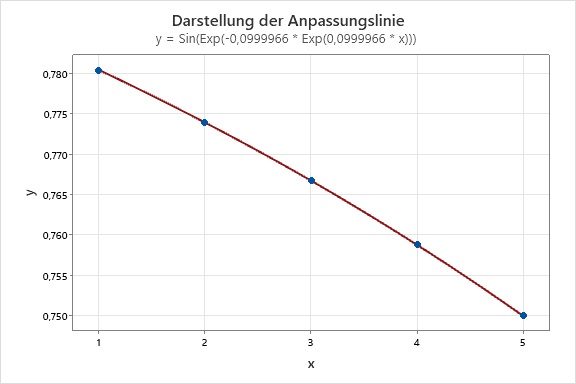
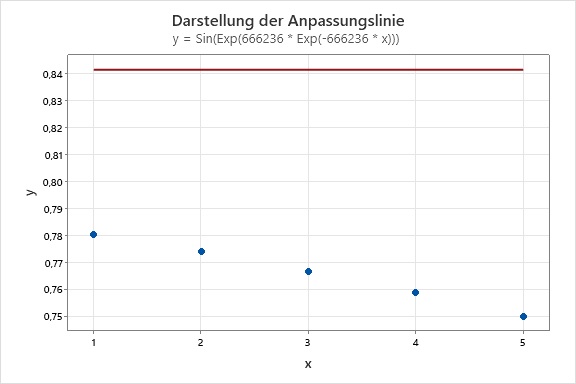
Im Gegensatz zum ersten Beispiel erhalten wir für die Nullstelle(n) der ersten Ableitung der Summe der Fehlerquadrate kein lineares Gleichungssystem. Wir können die Nullstelle also nicht beispielsweise mit dem Gauß-Algorithmus ermitteln. Wir müssen hier ein numerisches Verfahren heranziehen, für das wir einen Startwert vorgeben müssen. Wichtig ist, dass der Startwert geeignet gewählt wird. Hier sind zwei mögliche Ergebnisse. In dem einen Fall haben wir einen geeigneten Startwert für λ eingegeben, und der Wert für λ konvergiert gegen das lokale Minimum der Summe der Quadrate auf der oberen Grafik. In dem zweiten Beispiel haben wir einen nicht geeigneten Startwert für λ gefunden, und der Wert für λ konvergiert nicht gegen dieses lokale Minimum.
 |
 |
Anmerkung: In diesem Beispiel haben wir ein nichtlineares Modell gewählt, dass für diesen Datensatz vermutlich geeignet ist. Wenn das Modell nicht geeignet gewählt wird, kann es sein, dass die Fitparameter tatsächlich gegen ein lokales oder sogar globales Minimum der Summe der Fehlerquadrate konvergiert und der Fit trotzdem keine guten Prognosen für neue Beobachtungen innerhalb des Definitionsbereichs liefert.
|
|