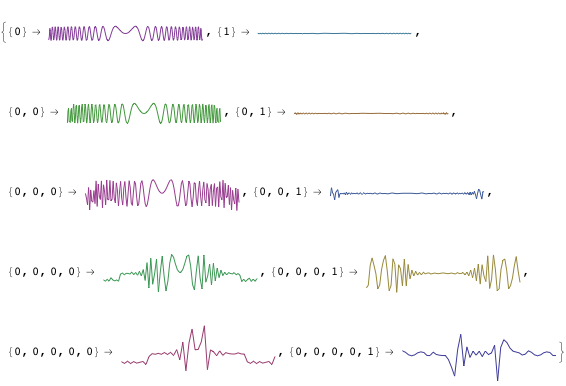
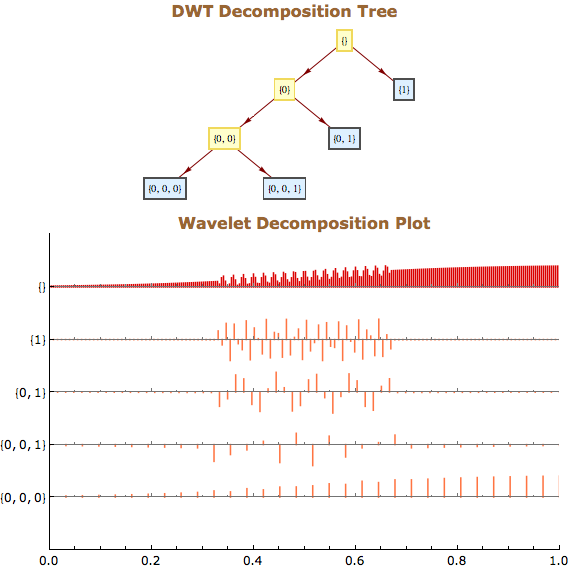
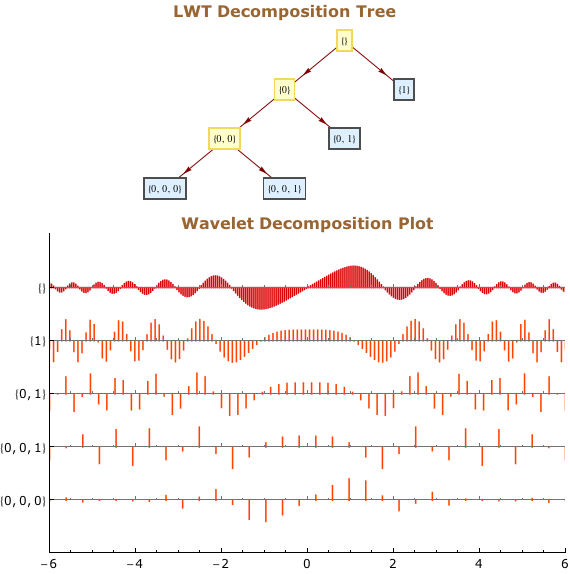
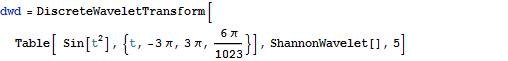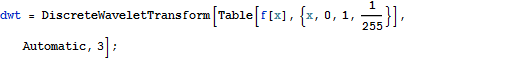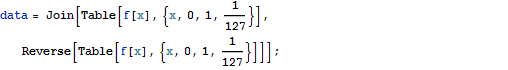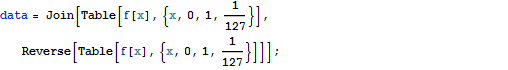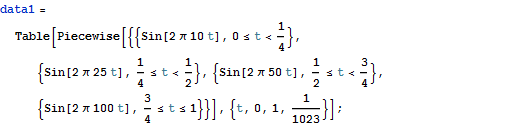Wavelet Analysen

In Mathematica 8 wird ein komplettes Paket an Wavelet Methoden in Mathematica eingeführt.
Wenden Sie diskrete oder kontinuierliche hochperformante Wavelet-Analysen für Berechnungen des Schwellenwerts und die Visualisierung an und das in beliebigen Dimensionen.

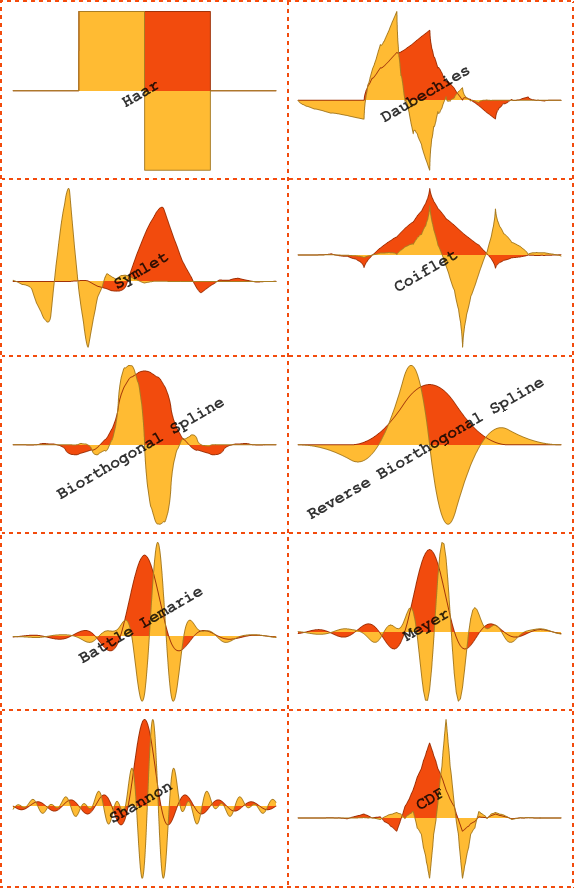
Darstellung vieler neuer diskreter Wavelet Funktionen
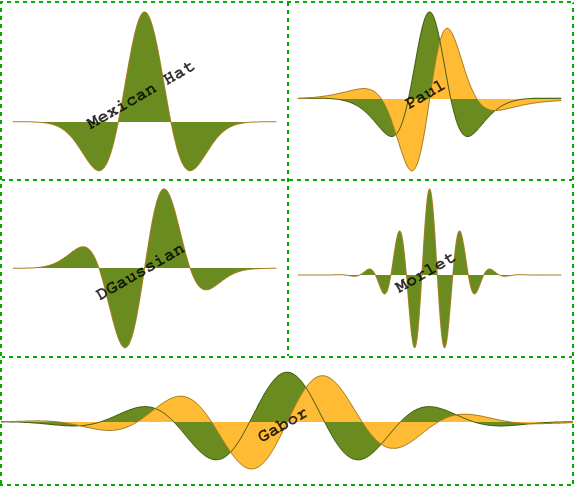
Darstellung vieler neuer kontinuierlicher Wavelet Funktionen
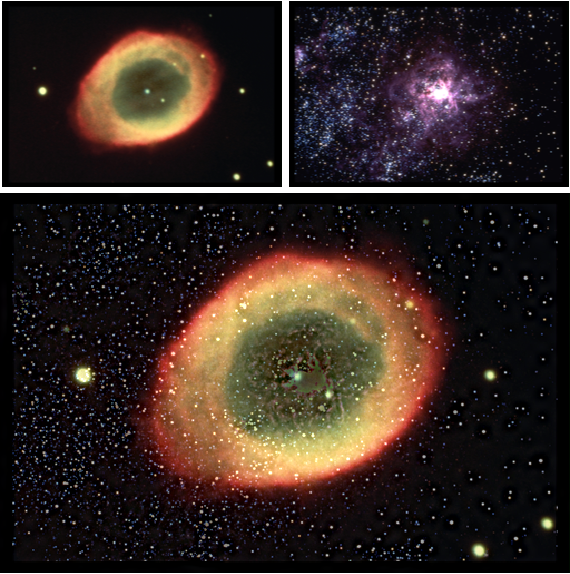
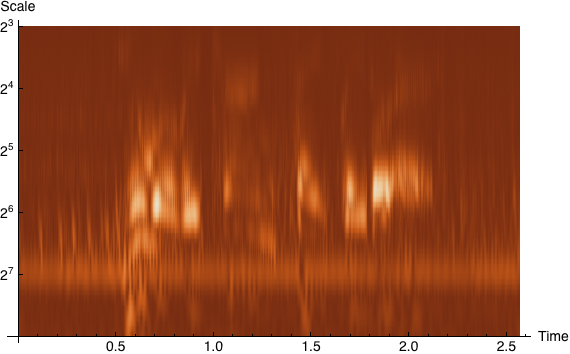
Signal- und Bildanalyse

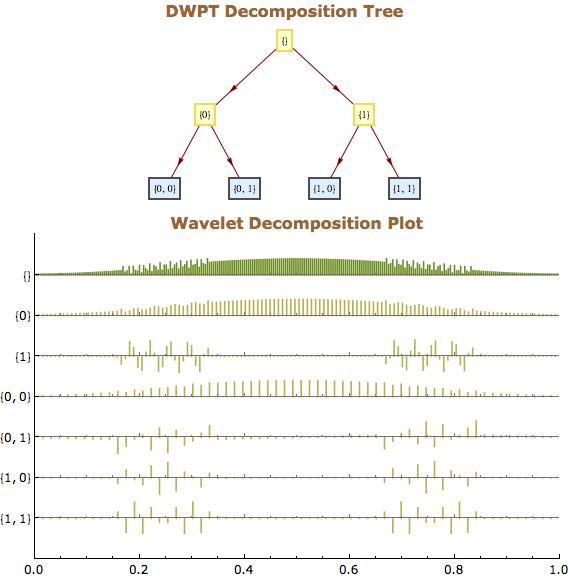
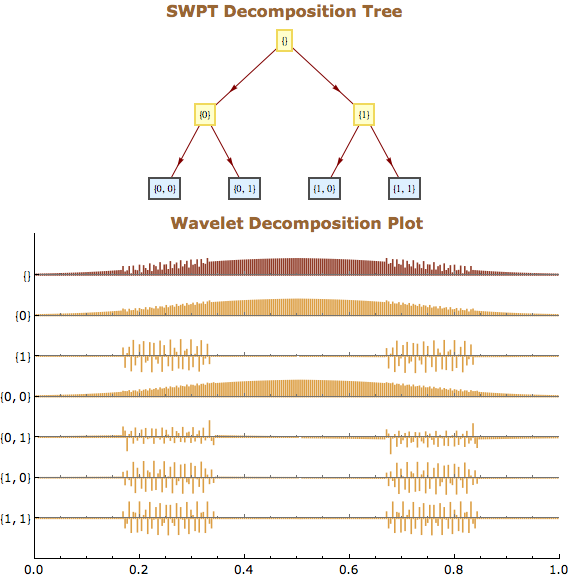
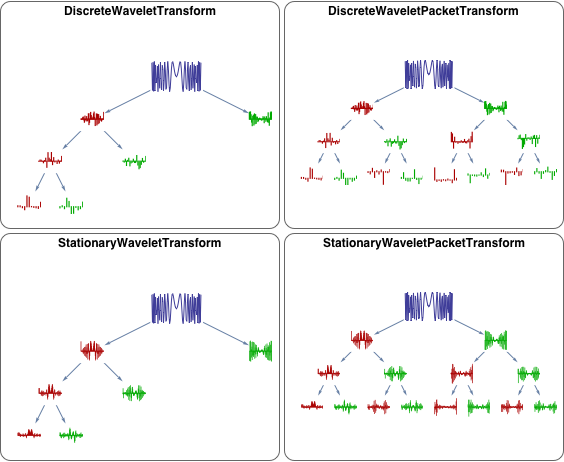
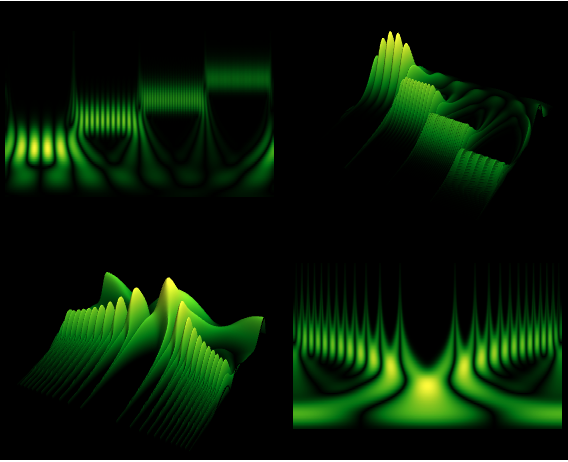
Der Anwender kann seine Daten in mehrere Wavelet-Basen transformieren, in Wavelet-Paket-Basen oder trigonometrische Basen und inverse Transformationen in einer oder zwei Dimensionen durchführen. Im Anschluss lässt sich die Transformation in einem Zeit-Frequenz-Raum darstellen und verschiedene Basen und Randbedingungen auswählen. Datenkompression und Entstören von Daten sind dabei überraschend einfache Vorgänge, die mit den eingebauten Funktionen des Wavelet-Paketes durchgeführt werden können.