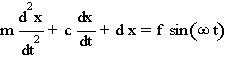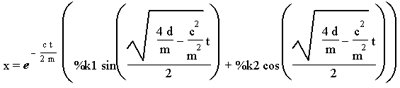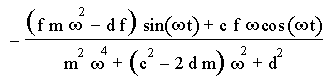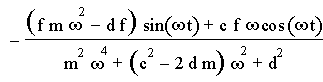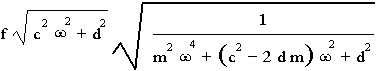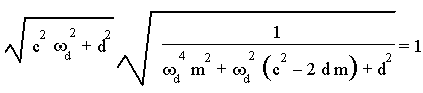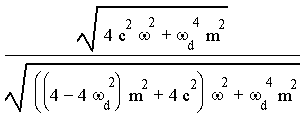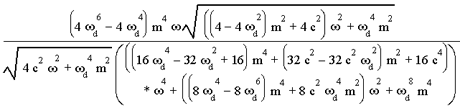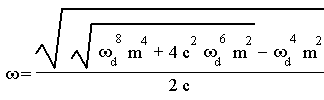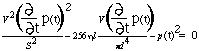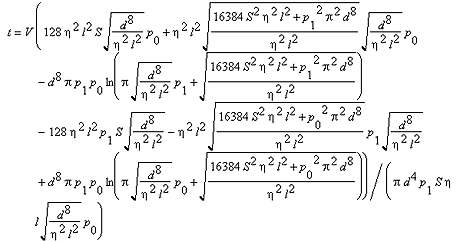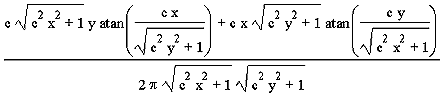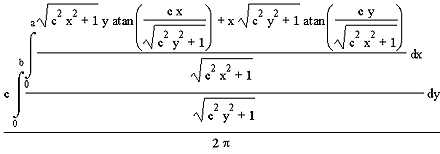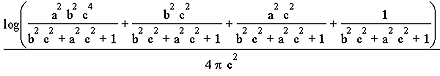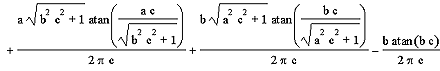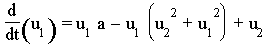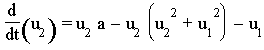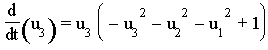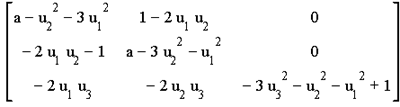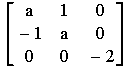Mathematica als Computeralgebra-System

Vorwort

Die Vorstellung und der Wunsch, Mathematik am Computer so betreiben zu können wie auf dem Blatt Papier, ist grundsätzlich nichts Neues und eigentlich ein allgemeines Anliegen. Ein jeder von uns weiß um die Beschwerlichkeit der rein mechanischen Ausführung von Berechnungen, welche die eigene Kreativität behindern, eine Menge Zeit kosten und nicht selten in einem Meer von Leichtsinnsfehlern enden (man erinnere sich nur einmal an das berühmte Vorzeichen, das plötzlich irgendwann verschwunden war). Nicht selten unterläßt man deswegen in der Praxis wichtige Berechnungen, auch wenn sie erfolgversprechend wären, nur weil der damit verbundene Arbeitsaufwand aus genannten Gründen zu hoch ist. Oder man hat einfach vergessen, wie das entsprechende Integral oder die entsprechende Differentialgleichung zu lösen ist. Bereits vor über 40 Jahren hat man deshalb die erste große Hürde in Angriff genommen und begonnen, Algorithmen (und damit auch Programme) zu entwerfen und stetig weiterzuentwickeln, die fehlerfrei die Mechanik der Mathematik beherrschen. Die Forschung auf diesem Gebiet hat sich mittlerweile zu einem eigenen Wissenschaftszweig namens Computeralgebra entwickelt, der auch einige eigens dafür konzipierte Lehrstühle hervorgebracht hat. Neben der rein algorithmischen Abstraktoion galt es bis vor wenigen Jahren allerdings noch eine zweite Hürde zu nehmen: Die benötigte Rechnerleistung war zu hoch und damit nicht bezahlbar und die Bedienung der Programme war, sagen wir einmal, "gewöhnungsbedürftig". Mit den neuen Rechnergenerationen und den modernen Benutzeroberflächen gehören diese Dinge der Vergangenheit an. Die modernen Computeralgebrasysteme haben sich zu einem absolut effizienten mathematischen Hilfsmittel entwickelt und werden ohne Zweifel an den Schreibtischen genauso Einzug halten, wie vor einigen Jahren der Taschenrechner. Man könnte Computeralgebrasysteme auch als sehr intelligente Taschenrechner bezeichnen.

Computeralgebra - Mathematik mit dem Computer

Stellen Sie sich einmal vor, Sie hätten alle Formeln ihrer Schulzeit, Ihres Studiums und Ihrer beruflichen Tätigkeit augenblicklich zur Verfügung. Zusätzlich würde diese Sammlung noch angereichert mit dem Wissen einer großen Zahl von hochqualifizierten Mathematikern, Ingenieuren, Physikern und anderen Naturwissenschaftlern. Außerdem hätten Sie noch jemanden an der Hand, der den Umgang mit all diesem Wissen intelligent handhabt, Ihnen die Schreibarbeit der Formeln abnimmt, Formelmanipulationen fehlerfrei durchführt, Differentiale und Integrale fehlerfrei bestimmt, Gleichungen löst, Grafiken zeichnet und Ergebnisse auf beliebige Genauigkeiten ausrechnet. Dies alles bietet Ihnen ein Computeralgebrasystem. Computeralgebra nutzt den Rechner nicht in erster Linie zur Berechnung von Zahlen, sondern zum optimalen Umgang mit Formeln.

Der Unterschied zur Handrechnung besteht darin, dass Rechnungen absolut verifizierbar sind, dass keine Beschränkung in der Größe von Ausdrücken besteht und dass Parameteränderungen sehr leicht durchgeführt werden können. Man kann mit Hilfe eines Computeralgebrasystems Lösungsansätze angehen, die man erst gar nicht in Erwägung ziehen würde, müsste man diese Berechnungen mit der Hand durchführen.

Computeralgebra in der Praxis

Textverarbeitungssysteme sind ein unumstrittenes und gern benutztes Hilfsmittel. Die Vorteile eines Textverarbeitungssystems liegen auf der Hand: Der Verfasser kann sich auf den Inhalt konzentrieren; Layout, Formatierung, Silbentrennung und Rechtschreibprüfung werden zuverlässig von der Textverarbeitung ausgeführt. Die Summe aller Hilfsmittel führt hier bei richtiger Anwendung ohne Zweifel zu gesteigerter Kreativität und Produktivität.

Analog verhält es sich mit Computeralgebrasystemen. Sie stellen alle Hilfsmittel zur Verfügung, die man benötigt, um zuverlässig, schnell und vor allem mathematisch korrekt Berechnungen durchführen zu können. Darüber hinaus werden zusätzliche Werkzeuge zur Verfügung gestellt wie elektronische Handbücher, dreidimensionale graphische Visualisierung und vorgefertigte Lösungsstrategien. Die Summe aller Hilfsmittel führt auch hier bei richtiger Anwendung ohne Zweifel zu einem produktiveren Arbeitsstil. Genau wie bei einer Textverarbeitung übernimmt der Rechner alle "Handarbeiten", der Anwender kann sich voll und ganz auf den mathematischen Gehalt konzentrieren. Die Schnittstelle zum Benutzer entspricht dabei dem gewohnten mathematischen Formelsatz, ausgeführte Berechnungen können mit Text kommentiert werden und haben durchgehend Dokumentationsqualität. Die Frage nach den praktischen Anwendungsmöglichkeiten hat sich damit weitgehend selbst beantwortet: Computeralgebrasysteme werden überall dort benötigt, wo mathematische Berechnungen, und zwar in jeder Form, durchgeführt und dokumentiert werden müssen, sowohl in der Industrie als auch in Wissenschaft und Forschung. Da einige Computeralgebrasysteme in Ihrem Leistungsumfang durchaus das Niveau einer Formelsammlung wie dem Bronstein erreichen, sind den Anwendungsmöglichkeiten praktisch keine Grenzen gesetzt.

Angefangen bei einfacheren Aufgaben wie der Berechnung von Schwerpunkten über die Berechnung von Temperaturgradienten in der Thermodynamik bis hin zur vollständigen dynamischen Durchrechnung von Mehrkörpersystemen sind mit Computeralgewbrasystemen alle Arten mathematischer Berechnungen realisierbar. Neben den geschilderten Möglichkeiten der dokumentierbaren algebraischen Formelmanipulation können Sie mit Computeralgebrasystemen auch numerische Berechnungen durchführen oder Meßdaten verarbeiten und graphisch visualisieren. Eine weitere Perspektive bietet sich mit der Sammlung hochkomplexer mathematischer Funktionen, die dem Anwender in der Regel über eine Programmiersprache zur Verfügung gestellt wird. Damit lassen sich durchaus Programme erstellen, die in einer herkömmlichen Programmiersprache erstellt den vielfachen Programmieraufwand gefordert hätten. An der Universität Kaiserslautern wurde mit einem Computeralgebrasystem ein Programm erstellt, das beliebig komplexe Analogschaltungen dimensioniert. Das Programm erstellt über einen graphischen Eingabesatz selbstständig die Gleichungen des Netzwerkes auf, berechnet symbolisch die Übertragungsfunktion und vereinfacht diese auf ein Minimum.

Insgesamt präsentieren sich Computeralgebrasysteme als hochleistungsfähige mathematische Universalwerkzeuge, die genau die gleiche Beachtung verdienen wie moderne Textverarbeitungssysteme.

Einige praktische Beispiele

Damit Sie sich ein richtiges Bild von Computeralgebrasystemen machen können, haben wir für Sie einige Beispiele mit Mathematica durchgerechnet. Die Eingaben haben wir uns aus Platzgründen geschenkt.

Lesen Sie auch den Artikel "Mathematische Modellentwicklung und Computer-Algebra-Simulation" (PDF, 85 KB)

Modifiziert übernommen aus "Computeralgebrasysteme". Mit freundlicher Genehmigung des Autors Stefan Braun (SmartCAE) und der ADDISON Wesley Longman Verlag GmbH.

Schwingungstilger

Eine Werkzeugmaschine wird durch eine rotierende Unwucht zu Schwingungen angeregt. Um die Halle auch nach längerer Zeit unbeschädigt vorzufinden, versucht man in der Regel, die Schwingungen zu tilgen. Die Maschine wird dazu auf einem federnden und dämpfenden Tilger aufgestellt. Die Dämpfung und Federung des Tilgers ist dabei so auszulegen, dass ein möglichst geringer Teil der Unwuchtkraft (Fu) auf das Fundament übertragen wird. Das Verhältnis der tatsächlich auf das Fundament wirkenden Kraft und der anregenden Kraft gibt Aufschluss über die Wirksamkeit der (falls vorhandenen) Schwingungstilgung und soll berechnet und qualitativ dargestellt werden.

Eine Tilgung der Anregung ist dann als solche definiert, wenn die auf das Fundament übertragene Kraft kleiner als die maximale durch die Unwucht erzeugte Kraft ist. Dieses Phänomen tritt erst ab einer bestimmten Kreisfrequenz auf. Vorher wird die Anregung von der Maschine noch verstärkt oder im günstigsten Falle gleich an das Fundament weitergegeben. Die Kreisfrequenz, ab der eine Tilgung vorliegt, wird alleinig durch die Federkonstante des Tilgers bestimmt. Für die maximale Amplitude der Maschine vor dieser Kreisfrequenz ist die Dämpfungscharakteristik des Tilgers verantwortlich. Im vorliegenden Fall ist die Federkonstante d des Tilgers nun so zu bestimmen, dass ab einer vorgegebenen Winkelgeschwindigkeit eine Tilgung eintritt. Bei einer vorgegebenen Dämpfungskonstante c ist diejenige Winkelgeschwindigkeit anzugeben, bei der die maximale Amplitude der Maschine erreicht wird. Gefragt sind auch die maximale Amplitude selbst sowie das Verhältnis zwischen Erregeramplitude und maximaler Maschinenamplitude. Das System wird durch die nachfolgende Bewegungsgleichung charakterisiert:

Das CA-System findet 3 Lösungen, den Kriechfall für starke Dämpfung, den aperiodischen Grenzfall und Schwingfall für schwache Dämpfungen. Wir bearbeiten die Lösung für schwache Dämpfungen weiter.

Da uns nur der eingeschwungene Zustand interessiert, betrachten wir nur die partikuläre (physikalisch stationäre) Lösung.

Nun berechnen wir die Kraft, die auf das Fundament übertragen wird. Diese Kraft ist durch

bestimmt. Dazu setzen wir die stationäre Lösung in die Gleichung für die gesuchte Kraft ein und werten diese aus. Damit erhalten wir für die Amplitude des Fundaments Am

Mit der Amplitude Af der Erregung erhalten wir ein Amplitudenverhältnis von

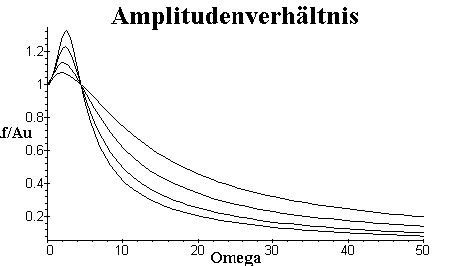
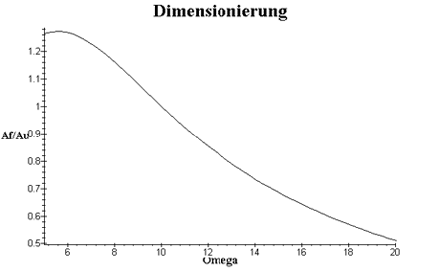
Jetzt stellen wir das Ampitudenverhältnis für eine Federkraft d=10000 N/m und eine Masse m=1000 kg und für verschiedene Dämpfungen von 4000 bis 10000 in Abhängigkeit von dar.

Danach berechnen wir die Kreisfrequenz, bei der das Amplitudenverhältnis gleich 1 ist. Dazu setzen wir den vorstehenden Ausdruck gleich 1 und für

Damit ergibt sich die Federkonstante zu . Wie Sie sehen, ist diese nicht von c abhängig. Danach setzen wir die Federkonstante in das Amplitudenverhältnis ein und erhalten das Verhältnis in Abhängigkeit der Konstanten .

Um die Kreisfrequenz zu bestimmen, bei der das Amplitudenverhältnis maximal wird, leiten wir den Ausdruck nach w ab und lösen die Ableitung nach auf.

Wir dimensionieren nun die Federkonstante mit der Gleichung so, dass ab einer Kreisfrequenz von 10 und einer Masse von m=1000 kg Maße eine Tilgung eintritt. Die Federkonstante beträgt damit 50000 Mit einer Dämpfungskonstanten von 10000 ergibt sich die Frequenz der maximalen Amplitude aus der letzten Gleichung zu 7,03 . Das maximale Amplitudenverhältnis ergibt sich damit zu 1.227

Modifiziert übernommen aus "Computeralgebrasysteme". Mit freundlicher Genehmigung der Authoren Stefan Braun und Harald Häuser (beide Visual Analysis GmbH) und der ADDISON Wesley Longman Verlag GmbH.

Auspumpen eines Rezipienten

Ein Rezipient mit dem Volumen V gefüllt mit einem Gas der Viskosität soll durch eine Vakuumpumpe evakuiert werden. Diese ist über eine Rohr der Länge l und dem Durchmesser d mit dem Rezipienten verbunden. Die Pumpe hat das konstante Saugvermögen S. Der Rezipient soll vom Druck p0 auf den Druck p1 evakuiert werden. Es ist die minimal mögliche Auspumpzeit des Behälters ohne Leck ql zu bestimmen und die Auspumpzeit in Abhängigkeit von der Saugstärke der Pumpe. Die Auspumpzeit soll dann in Abhängigkeit vom Saugvermögen der Pumpe dargestellt werden. Als praktische Werte setzen wir , , l=1 m und d=0.1 m. Der Rezipient soll von auf evakuiert werden. Die Differentialgleichung für den Auspumpvorgang ohne Leck lautet:

Als Lösung liefert das CA-System:

Jetzt berechnen wir die minimal erreichbare Auspumpzeit. Dazu lassen wir in der Lösung der Differentialgleichung das Saugvermögen unendlich groß werden. Die minimale Auspumpzeit t ergibt sich damit zu

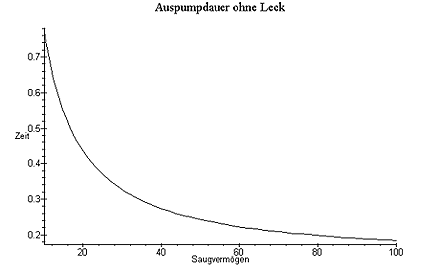
Um uns eine qualitative Vorstellung von der Abhängigkeit der Auspumpzeit vom Saugvermögen zu machen, stellen wir die Auspumpzeit in Abhängigkeit der Pumpenstärke graphisch dar. Sehr deutlich können Sie hier die asymptotische Annäherung an die Auspumpzeit von 0.138 s erkennen.

Modifiziert übernommen aus "Computeralgebrasysteme". Mit freundlicher Genehmigung der Authoren Stefan Braun und Harald Häuser (beide Visual Analysis GmbH) und der ADDISON Wesley Longman Verlag GmbH.

Wärmestrahlung

Eine Seite eines rechteckigen, mit flüssigem Wasserstoff gefüllten Tanks ist durch eine Vakuumisolierung nach außen hin isoliert. Auf der anderen Seite der Isolierung befindet sich flüssiger Stickstoff. Die Temperatur des Wasserstoffs ist , die Temperatur des Stickstoffs ist . Der Abstand der beiden Platten ist so zu wählen, dass der Wärmestrom 30 W nicht übersteigt. Beide Platten sind quadratisch mit einer Seitenlänge von 1 m und metallisch mit Aluminium bedampft. Sie haben ein Emissionsgrad von .

Der von der Fläche mit der höheren absoluten Temperatur an die Fläche mit der niedrigeren absoluten Temperatur durch Wärmestrahlung transportierte Wärmestrom beträgt , wobei mit der Maßeinheit der Strahlungsaustauschkoeffizient ist. Aus der Bilanz der ausgetauschten Strahlungsleistungen zwischen beiden grauen Körpern ergibt sich für den Strahlungsaustauschkoeffizienten

wobei und die Emissionszahlen der beiden Platten sind. ist die Stefan-Boltzmannkonstante und eine von der Geometrie abhängige Einstrahlzahl. Die Berechnung dieser Einstrahlzahl ist in der Regel schwierig, da dazu mehrere Integrationen notwendig sind. Der Austauschkoeffizient zwischen einem infinitisimalen Element und der Platte beträgt

wobei die Variable c den Abstand zwischen beiden Platten charakterisiert. Wir bilden jetzt das Integral über die Platte . Die Begrenzungen der Platte sind die Seitenlängen a und b.

Wenn wir dieses Integral auswerten, erhalten wir für die Einstrahlzahl

Wir setzen nun die Einstrahlzahl in die Gleichung von ein. Auf die Darstellung des Zwischenergebnisses verzichten wir hier. Wir setzten nun die Zahlenwerte ein und lösen die resultierende Gleichung numerisch nach c auf. Dadurch erhalten wir einen Abstand von 0.56 m.

Modifiziert übernommen aus "Computeralgebrasysteme". Mit freundlicher Genehmigung der Autoren Stefan Braun und Harald Häuser (beide Visual Analysis GmbH) und der ADDISON Wesley Longman Verlag GmbH.

Chemisches Gleichgewicht

Die Dynamik eines chemischen Raktionssystems wird durch ein System von nichtlinearen Differentialgleichungen beschrieben. Von besonderem Interesse sind bei derartigen Systemen die stabilen Zustände, d.h die Punkte an denen die Konzentrationsänderungen Null sind. Das chemische Reaktionssystem wird durch die nachfolgenden drei Differentialgleichungen beschrieben.

Zuerst bestimmen wir die stationären Punkte. Dazu setzen wir alle Ableitungen zu Null.

Dieses nichtlineare Gleichungssystem lösen wir nun nach den einzelnen Konzentrationen auf. Dadurch erhalten wir die stationären Punkte des Gleichgewichts: u1=0, u2=0 und u3=1. Alle anderen Lösungen scheiden aus physikalischen Gründen aus. Sie können hier auch erkennen, dass der Parameter a keinen Einfluß auf den Gleichgewichtspunkt hat. Abschließend wollen wir noch wissen, ob es sich um ein stabiles oder instabiles Gleichgewicht handelt. An der Stelle des stationären Punktes untersuchen wir dazu die Eigenwerte des linearisierten Differentialgleichungsystems, das der Jacobimatrix entspricht. Zur Bestimmung der Eigenwerte setzen wir den stationären Punkt in die Jacobimatrix des Systems ein. Die Jacobimatrix des Systems lautet:

Die Eigenwerte der Matrix ergeben sich zu

Das System ist dann stabil, wenn die Realteile aller Eigenwerte kleiner als Null sind. Die Eigenwerte der Matrix sind -2 und a. Das System zeigt also nur stabiles Verhalten, wenn a<0 ist.

Modifiziert übernommen aus "Computeralgebrasysteme". Mit freundlicher Genehmigung der Authoren Stefan Braun und Harald Häuser (beide Visual Analysis GmbH) und der ADDISON Wesley Longman Verlag GmbH.