Mathematica und Cuda
Über das integrierte CUDALink Paket liefert Mathematica Unterstützung für die Grafikprozessorprogrammierung für grafikprozessorbeschleunigte lineare Algebra, diskrete Fourier-Transformationen und Bildverarbeitungsalgorithmen. Bei Bedarf können Sie CUDALink Module auch ganz einfach selbst schreiben.
Das CUDALink Paket von Mathematica liefert folgende Funktionen ganz ohne zusätzliche Kosten:
- Zugriff auf die automatischen Interface-Builder, Import/Export-Funktionen und Visualisierungsfunktionen von Mathematica
- Zugriff auf die betreuten Mathematica Datenbanken
- Unterstützung für Arithmetik mit einfacher und doppelter Genauigkeit
- Möglichkeit, benutzerdefinierte CUDA Programme in Mathematica zu laden
- Skalierbarkeit für mehrere Geräte
- Integration mit existierenden Mathematica Technologien wie Remote Sessions
Mehr Infos zu High Performance Computing mit Wolfram Mathematica.
Weitere Ressourcen: Mathematica GPU Computing Leitfaden
Mathematica GPU Computing Leitfaden Mathematica CUDALink Tutorial
Mathematica CUDALink Tutorial Mathematica OpenCLLink Tutorial
Mathematica OpenCLLink Tutorial CUDA Programmierung in Mathematica – Wolfram Whitepaper
CUDA Programmierung in Mathematica – Wolfram Whitepaper
CUDA Bausteine
Einleitung
Die "Common Unified Device Architecture" (CUDA) wurde im Jahre 2007 von NVIDIA entwickelt. Auch wenn es die Programmierung der GPU schon seit Jahren gibt, haben Hardwarerestriktionen das Schreiben von Software für die Grafikkarte nicht leicht gemacht. Eine Aufgabe von CUDALink von Mathematica ist es, das Programmieren und die Portierung der eigenen Software zu vereinfachen. Wenn man Mathematica benutzt, muss man sich keine Gedanken über die vielen Hürden machen. Somit bleibt das Hauptaugenmerk auf dem Schreiben der CUDA Kernel. Das wird durch durch Nutzen aller NVIDIA Architektur Stacks bewerkstelligt.
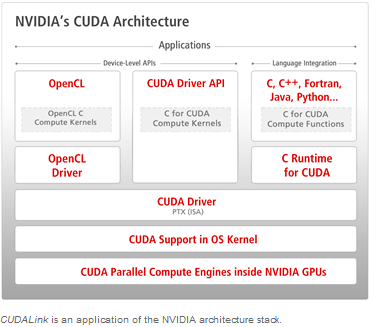
Architektur
Hier der schematische Aufbau der CUDA Architektur.
Grid und Blocks
CUDA-Programmierung basiert auf dem Daten-Parallelisierungs-Modell. Berechnungen werden auf viele hundert - wenn nicht gar tausend Threads geteilt. Wenn Folgendes Ihre Berechnung wäre:
OutputData = Table[fun[InputData[[i, j]]], {i, 10000}, {j, 10000}]|
, dann wäre dies hier Ihr CUDA-Äquivalent: |
wobei "fun" Ihre selbst definierte Funktion ist. Das Beispiel startet 1000 x 1000 Threads und übergibt jedem deren Indizes. Das Ergebnis wird InputData zugewiesen und in OutputData gespeichert.
Der Grund, weshalb CUDA Tausende von Threads starten können, liegt an der Hardwarearchitektur. Im folgenden Abschnitt erörtern wir nun, wie Threads geteilt werden.
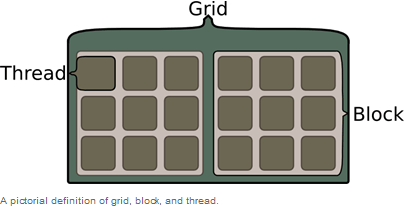
CUDA teilt programmatische Probleme in ein-, zwei- oder dreidimensionale Grids auf. Folgendes Bild zeigt eine typische zweidimensionale CUDA-Thread-Konfiguration.
Jedes Grid beinhaltet mehrere Blöcke, und jeder Block besteht aus Threads. Ausgehend von dem obigen Bild, kann man sich die Grids, Blocks und Threads wie folgt vorstellen.
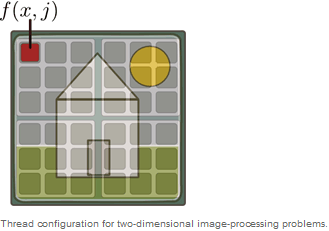
Ob man nun eine ein-, zwei- oder dreidimensionale Thread-Konfiguration verwendet, ist abhängig von dem Problem. Im Fall von Bildbearbeitung mappen wir die Threads wie in dem Bild und weisen jedem Pixel eine Funktion zu.
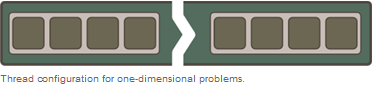
Der eindimensionale zelluläre Automat kann auf ein eindimensionales Grid gemappt werden.
Program Cycle
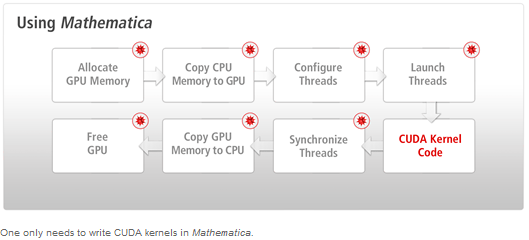
Das Wesentliche an der CUDA-Programmierung sind folgende drei Schritte:
- Kopieren der Daten beim Starten der Threads
- Warten, bis die GPU die Berechnung durchgeführt hat
- Kopieren des Ergebnisses von der GPU zum Host
- Zuteilen des Arbeitsspeichers der GPU: GPU- und CPU-Speicher sind physikalisch getrennt, und der Programmierer muss die zugewiesenen Kopien verwalten.
- Der Speicher wird von der CPU zur GPU kopiert.
- Konfigurieren der Thread-Konfiguration: Der korrekte Block und die Grid-Dimension für das Problem werden ausgewählt.
- Die konfigurierten Threads werden gestartet.
- Durch die Synchronisation der CUDA-Threads wird sicher gestellt, dass die GPU alle Aufgaben beendet hat, um dann weitere Operationen auf dem Speicher der GPU auszuführen.
- Wenn die Operationen ausgeführt wurden, wird der Speicher von der GPU auf die CPU wieder zurückgeschrieben.
- Der GPU-Speicher wird geleert.
Wenn Mathematica genutzt wird, muss man sich über die vielen verschiedenen Schritte keine Gedanken mehr machen, sondern kann sich auf das Schreiben des CUDA Kernels konzentrieren.
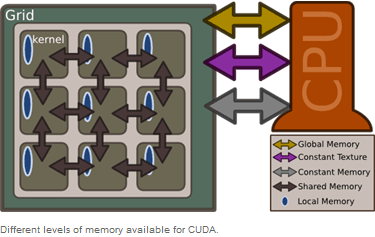
Speicher-Hierarchie
CUDA-Speicher wird in verschiedene Bereiche getrennt; jeder dieser Speicherbereiche hat seine Vorteile und Beschränkungen. Das folgende Bild zeigt alle Typen von CUDA-Speicher.
Global Memory
Der Arbeitsspeicher beansprucht den größten Raum auf einer Grafikkarte und ist dabei auch am langsamsten. Alle Threads können Speicher aus dem "Global Memory" nehmen. Dies sollte man aber aus Gründen der Performance, wenn möglich, vermeiden.
Texture Memory
Das "Texture Memory" residiert in demselben Bereich wie das "Global Memory", ist aber nur lesbar. Dafür ist es sehr viel performanter. Dieser Speicher unterstützt nur die Werte string, char und int unterstützt.
Constant Memory
Hierbei handelt es sich um einen schnellen Speicher, der für jeden Thread aus dem Grid verfügbar ist. Der Speicher wird gecached, ist aber global auf 64 kB limitiert.
Shared Memory
Auch dies ist ein schneller Speicher, der mit jeweils einem Block verbunden ist. Unter aktueller Hardware ist dieser Speicher auf 16kB pro Block limitiert.
Local Memory
Dieser Speicher ist für jeden Thread lokal, residiert aber im "Global Memory", bis der Kompiler die Variablen in das Register schreibt. Auch hier sollte man die Zugriffe auf ein Minimum beschränken, selbst wenn dieser Speicher nicht ganz so langsam wie das "Global Memory" ist.
Compute Capability
Die "Compute Capability" gibt an, was die verwendete Hardware für Operationen unterstützt. Zurzeit sind folgende verfügbar:
| Compute Capability: |
Extra Features: |
| 1.0 | base implementation |
| 1.1 | atomic operations |
| 1.2 | shared atomic operations and warp vote functions |
| 1.3 | support for double-precision operations |
| 2.0 | double precision, L2 cache, and concurrent kernels |
Sollten Sie CUDALink noch nicht importiert haben, holen Sie dies bitte jetzt nach:
Needs["CUDALink`"]
Folgender Befehl zeigt alle CUDA-fähigen Komponenten Ihres Systems an:
TabView[Table[
CUDAInformation[ii, "Name"] ->
CUDAInformation[ii,
"Compute Capabilities"], {ii, $CUDADeviceCount}]]
CUDA Devices
Wenn die Systemhardware es erlaubt, lässt CUDA den Anwender entscheiden, auf welcher GPU die Berechnungen durchgeführt werden sollen. Standardgemäß wird die schnellste genutzt, aber diese Einstellung kann von dem Benutzer außer Kraft gesetzt werden. Sobald eine GPU ausgewählt wurde, kann diese während der Kernel Session nicht mehr verändert werden.
Kernel erstellen
Der erste Kernel
CUDA Kernel sind atomare Funktionen, die die Berechnung auf jedes Element einer Eingabeliste durchführen. Unser erster Kernel wird 2 Elemente miteinander addieren.
__global__ void addTwo_kernel(int * arry, int len) {int index = threadIdx.x + blockIdx * blockDim.x;
if (index >= len) return;
arry[index] += 2;
}
__global __ ist ein Funktionsqualifizierer, der dem Compiler mitteilt, dass diese Funktion auf der GPU ausgeführt werden soll. __global__ functions kann direkt aus C heraus aufgerufen werden. Die andere Funktion ist __device__, welche Funktionen definiert, die von anderen Funktionen wie __global__ oder __device__ aufgerufen werden können, aber nicht von C.
Ein CUDA Kernel muss "void"-Ausgabe besitzen; um ein Ergebnis zu erhalten, müssen daher die Input Pointer überschrieben werden. In diesem Fall übergeben wir ein Array und überschreiben die Elemente (hier kann man sich vorstellen, dass das Array die Eingabe/Ausgabeparameter besitzt)
int index = threadIdx.x+blockIdx*blockDim.x;
Mit dem obigen Source Code erhalten wir den Index. Der CUDA Kernel stellt uns folgende Variablen zur Verfügung, die abhängig von dem auszuführenden Grid und der Blockgröße gesetzt werden.
- threadIdx - Index des aktuellen Threads; der Threadindex liegt zwischen 0 und blockDim -1
- blockIdx - Index des aktuellen Blocks; der Blockindex liegt zwischen 0 und gridDim -1
- blockDim - die Dimension der Blockgröße
- gridDim - die Dimension der Gridgröße
Diese Parameter werden von CUDA automatisch gesetzt in Abhängigkeit der Parameter, die beim Kernel-Start übergeben werden (die Block- und Griddimension). Höhere Dimensionen werden automatisch auf 1 gesetzt, wenn man eine Berechnung mit niedrigeren Dimensionen startet. Wenn man somit eine eindimensionale Berechnung ausführt, werden .y und .z auf 1 gesetzt.
In den meisten Fällen benutzt man in einem 1D-Grid threadIdx.x + blockIdx.x * blockDim.x, um das globale Offset zu finden. Um die globale Position in 2D zu erhalten, benutzt man threadIdx.x + blockIdx.x * blockDim.x + (threadIdx.y + blockIdx.y * blockDim.y)*width.
if (index >= len) return;
Da Threads im Mehrfachen der Blockdimension ausgeführt werden, muss sich der Anwender vergewissern, die Grenzen nicht zu überschreiben, sofern die Eingabedimension nicht das Mehrfache der Blockdimension ist. Dies wird sichergestellt durch:
in[index] += 2;
Diese Funktion wird auf jedes Element der Liste angewandt; hier wird 2 zu jedem Element addiert.
Der zweite Kernel
Der zweite Kernel implementiert eine finite Differenziermethode
__device__ float f(float x) {
return tanf(x);
}
__global__ void secondKernel(float * diff, float h, int listSize) {
int index = threadIdx.x + blockIdx.x * blockDim.x;
float f_n = f(((float) index) / h);
float f_n1 = f((index + 1.0) / h);
if( index < listSize) {
diff[index] = (f_n1 - f_n) / h;
}
}
Dies ist eine Device Funktion. __device__ Funktionen können von der __global__ Funktion aufgerufen werden, sind aber nicht aus Mathematica direkt ausführbar.
return tanf(x);Durchführung des Tangens auf eine float-Eingabe.
__global__ void secondKernel(float*diff, float h, int listSize) {Funktion, die die Liste diff ausgibt und die skalaren Größen h und listSize entgegen nimmt.
int index=threadIdx.x+blockIdx.x*blockDim.x;Liefert den globalen Thread Offset.
float f_n=f(((float) index)/h);Evaluiert die Funktion bei Index/h. Da Index und h vom Typ int sind, müssen wir das Ergebnis nach float konvertieren, um einen Abbruch zu vermeiden.
float f_n1=f((index+1.0)/h);Evaluiert die Funktion bei (index+1)/h.
if(index<listSize) {Verhindert das Überschreiben des Ausgabebuffers.
diff[index]=(f_n1-f_n)/h;Berechnet die Differenz und speichert das Ergebnis in diff.
Kernel laden
Kernel in Mathematica laden
Sollten Sie den CUDALink noch nicht geladen haben, holen Sie dies bitte jetzt nach.
Needs["CUDALink`"]Nun speichern wir den erstellten Code in einen string.
secondKernelCode = "__device__ float f(float x) {
return tanf(x);
}
__global__ void secondKernel(float * diff, float h, int listSize) {
int index = threadIdx.x + blockIdx.x * blockDim.x;
float f_n = f(((float) index) / h);
float f_n1 = f((index + 1.0) / h);
if( index < listSize) {
diff[index] = (f_n1 - f_n) / h;
}
}";
Dies lädt die CUDA-Funktion. Wir übergeben den Kernel-Code als erstes Argument, den Kernel-Namen, welcher ausgeführt wird ("secondKernel"), als zweites Argument, die Funktionsparameter als drittes Argument und die Blockgröße als viertes Argument. Das Ergebnis wird in secondKernel gespeichert.
secondKernel =
CUDAFunctionLoad[secondKernelCode,
"secondKernel", {{"Float"}, "Float", _Integer}, 16]
Im Hintergrund passieren folgende Dinge:
- CUDA-Verfügbarkeit wird geprüft.
- Der CUDA-Code wird zu einem Binary kompiliert und für die jeweilige GPU optimiert.
- Der CUDA-Code wird gecached, um später Kompilierung zu verhindern.
- Es wird geprüft, ob der Kernel aus dem CUDA-Code existiert.
Einmal geladen, kann die CUDA-Funktion wie eine Mathematica-Funktion benutzt werden. Bevor wir starten können, benötigen wir einen Speicher, in dem das Ergebnis abgelegt wird.
buffer = CUDAMemoryAllocate["Float", 1024]
Hier führen wir den zweiten CUDA Kernel aus.
secondKernel[buffer, 100.0, 1024]
Mit dem folgenden Befehl erhalten wir die ersten 30 Elemente aus dem Ausgabebuffer.
CUDAMemoryGet[buffer][[;; 30]]

Dies zeichnet unser Ergebnis:
ListPlot@CUDAMemoryGet[buffer]
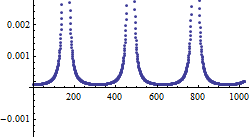
Der Buffer muss vom Benutzer wieder gelöscht werden.
CUDAMemoryUnload[buffer];
Systemanforderung
Systemanforderung
Zur Verwendung von Mathematica's CUDALink ist erforderlich:- Betriebssystem: Windows, Linux oder Mac OS X, 32-Bit oder 64-Bit Architektur
- NVIDIA CUDA-fähige Produkte
- Mathematica 8.0 oder besser
Die leistungsfähigen GPU Computing Funktionen von Mathematica wurden auf Tesla und Quadro GPU Computing Produkten entwickelt und erfordern aktuelle CUDA-fähige NVIDIA Grafikprozessoren.
Tesla und Quadro GPU Computing Produkte werden
speziell für maximale Rechenleistung und höchste numerische Präzision entwickelt und werden von führenden Herstellern professioneller Systeme angeboten und unterstützt.