Gaussian
Gaussian provides state-of-the-art capabilities for electronic structure modeling and is licensed for a wide variety of computer systems.Gaussian is an electronic structure program, used by chemists, chemical engineers, biochemists, physicists and other scientists worldwide, and provides a wide-ranging suite of the most advanced modeling capabilities available. You can use it to investigate the real-world chemical problems that interest you, in all of their complexity, even on modest computer hardware.
Starting from the fundamental laws of quantum mechanics, Gaussian predicts the energies, molecular structures, vibrational frequencies and molecular properties of compounds and reactions in a wide variety of chemical environments. Gaussian's models can be applied to both stable species and compounds which are difficult or impossible to observe experimentally, whether due to their nature (e.g., toxicity, combustibility, radioactivity) or their inherent fleeting nature (e.g., short-lived intermediates and transition structures).
With Gaussian, you can thoroughly investigate the chemical problems that interest you. For example, not only can you minimize molecular structures rapidly and reliably, you can also predict the structures of transition states, and verify that the predicted stationary points are in fact minima or transition structure (as appropriate). You can go on to compute the reaction path by following the intrinsic reaction coordinate (IRC) and determine which reactants and products are connected by a given transition structure. Once you have a complete picture of the potential energy surface, reaction energies and barriers can be accurately predicted. You can also predict a wide variety of chemical properties.
What Sets Gaussian Apart from Other Programs?
- Gaussian produces accurate, reliable and complete models without cutting corners.
- A wide variety of methods makes Gaussian applicable to a broad range of chemical conditions, problem sizes and compounds.
- Gaussian provides state-of-the-art performance in single CPU, multiprocessor/multicore and cluster/network computing environments.
- Setting up calculations is simple and straightforward, and even complex techniques are fully automated. The flexible, easy-to-use options give you complete control over calculation details when needed.
- Results from all calculation types are presented in natural and intuitive graphical form by GaussView.
Comprehensive Investigations
Comprehensive Investigations of Molecules and Reactions
With Gaussian, you can thoroughly investigate the chemical problems that interest you. For example, not only can you minimize molecular structures rapidly and reliably, you can also predict the structures of transition states, and verify that the located stationary points are in fact minima and transition states. You can go on to compute the reaction path by following the intrinsic reaction coordinate (IRC) and determine which reactants and products are connected by a given transition structure. Once you have a complete picture of the potential energy surface, reaction energies and barriers can be accurately predicted.
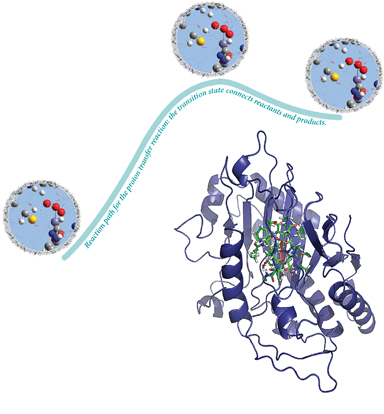
Researchers have used these fundamental capabilities of Gaussian to study isopenicillin N synthase (IPNS), a member of a family of mononuclear nonheme iron enzymes (illustrated at the bottom right of the next image). Transition metal enzymes catalyze some of the most important biochemical processes, and they can also serve as inspiration for novel biomimetic catalysis. In the latter context, these researchers wanted to determine how the metal center and the protein matrix separately contribute to the enzyme system's catalytic activity. They analyzed the catalytic mechanism of IPNS, exploring the potential energy surface for the transformation of the tripeptide substrate d-(l-a-aminoadipoyl)-l-cysteinyl-d-valine (ACV) to isopenicillin N (IPN). The ONIOM facility in Gaussian enables the transition structures and reaction paths to be computed for the reactions involving large proteins like this system.
The reactants (left), transition structure (center) and products (right), as well as the IRC reaction path, are all computed using the ONIOM facility. The highlighted inset focuses on the active atoms in the high accuracy layer, treated with density functional theory. The grey region outside is a tiny portion of the low accuracy layer, treated with molecular mechanics in the integrated QM:MM method.
A small part of their results are shown in the illustration above depicting the reactants, products and transition structure for a proton transfer reaction. Overall, their analysis suggests that the main catalytic effect comes from the metal center while the protein environment controls the high product specificity.
Predicting and Interpreting
Predicting and Interpreting Spectra
Spectroscopy is a fundamental tool for investigating molecular structures and properties. However, observed spectra are often difficult to interpret. The results of electronic structure calculations can be vital to this process. For example, predicted spectra can be examined in order to determine peak assignments in observed spectra as well as comparing peak locations and intensities with experimental data. Gaussian can also compute relevant spectroscopic constants and related molecular properties with excellent accuracy. This combination of experimental observation and theoretical computation can yield very accurate structural and spectral data for compounds of interest.
Gaussian can predict a variety of spectra including IR and Raman, NMR, UV/Visible, Vibrational circular dichroism (VCD), Raman optical activity (ROA), Electronic circular dichroism (ECD), Optical rotary dispersion (ORD), Hyperfine spectra (microwave spectroscopy), Franck-Condon, Herzberg-Teller and Franck-Condon/Herzberg-Teller analyses.
Modeling NMR
Gaussian continues to enhance the program's NMR capabilities. Spin-spin coupling constants are one of the most difficult spectral data to produce quantitatively. The accuracy of calculations is highly dependent on the basis set used. While the standard basis sets of quantum chemistry are well developed for valence electrons, a more sophisticated description of the electron density closer to the nuclei is needed for predicting the Fermi contact (FC) term (often the spin-spin coupling constants' largest component). Researchers at Gaussian, Inc. have explored this problem in depth and have developed modified basis sets suitable for modeling these quantities within a DFT framework; their results are summarized below. When requested, Gaussian will automatically perform a two-step calculation for NMR spin-spin coupling, using the standard basis set for the general calculation and the corresponding modified basis set for the FC term.
| Basis Sets for Computing NMR Spin-Spin Coupling Constants | ||
|---|---|---|
| Basis Set | Derived from | Accuracy Improvement |
| uTZ-w | aug-cc-pVTZ | 650% (?AAE=-20 Hz, AAE=3.6 Hz) |
| uDZ-w | aug-cc-pVDZ | 590% (?AAE=-41 Hz, AAE=8.7 Hz) |
| uG-w | 6-311+G(d,p) | 415% (?AAE=-33 Hz, AAE=10.3 Hz) |
Larger improvement percentages are better (AAE: average absolute error with respect to the basis set limit). Recommended basis sets are arranged from largest (top) to smallest.
Reference: W. Deng, J.R. Cheeseman & M.J. Frisch, JCTC 2 (2006) 1028.
Studying Chirality
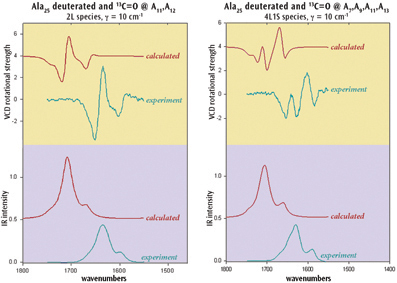
Chiral molecules are of great importance in many research contexts. Gaussian 09 can study chirality with several techniques including two of the latest spectroscopic classes: VCD and ROA. For example, researchers have used the VCD facility to model helical peptides. The structures of peptides composed of alanine are dominantly a-helical with the C terminus being coil-like. VCD experiments used isotopic labeling to demonstrate that the a-helix in Ala20 and in Ala25 (shown right) noncooperatively unwinds from the ends with increasing temperature.
The IR and VCD spectra for these systems were studied in solution with Gaussian 09. Results for Ala25 appear below. The calculations successfully reproduce the experimental observations and are additionally able to quantify the degree of "fraying." They also indicate that confidence can be placed in the reported molecular structures.
Experimental References: R. Silva, J. Kubelka, P.
Bour, S. Decatur and T. Keiderling,
PNAS 97 (2000) 8313; R. Huang, J. Kubelka, W. Barber-Armstrong, R. Silva, S. Decatur
and T. Keiderling, JACS 126 (2004) 2346. Computational reference in preparation.
Predicting Optical Spectra
Steady-state spectroscopy is one of the most fundamental tools for investigating equilibrium structures and potential energy surfaces for different electronic states. However, interpreting such experimental data is often not straightforward. Such situations often benefit greatly from calculations which aid in interpreting and assigning each spectral feature.
Several Gaussian capabilities in such studies. For example, the time-dependent DFT method produces high quality descriptions of excited state systems (comparable to DFT for the ground state), and Franck-Condon and Herzberg-Teller analyses can be used for computing the amplitudes for electronic transitions from the ground and excited state frequency analyses. The combination of the two can be used to effectively treat both transitions with large oscillator strengths and forbidden transitions. Solvation effects can be included in these models.
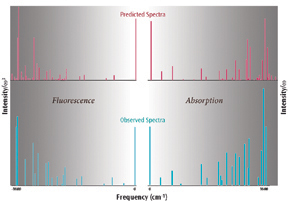
These methods have been used to compute the Herzberg-Teller absorption and fluorescence Qx spectra of free-base porphyrin. Their results are shown to the right. These graphs compare the high definition quasiline absorption and emission bands, plotting the computed and experimental intensities divided by? (absorption) or?3 (emission), and demonstrate excellent agreement.
Reference: F. Santoro, A. Lami, R. Improta, J. Bloino & V. Barone, J. Chem. Phys. 128 (2008) 224311.
Predicting Hyperfine Spectra
Gaussian computes the most important tensors which contribute to hyperfine spectra. Calculations can suggest regions in which to look for transitions, which can make experiments more efficient. Theoretical results are also useful for making spectral assignments for observed peaks, which can be difficult or impossible to determine solely from the raw experimental data. Computed tensors can also be combined with observations in fitting operations. Using computations to aid in interpreting and fitting observed results should make non-linear molecules as amenable to study as linear ones.
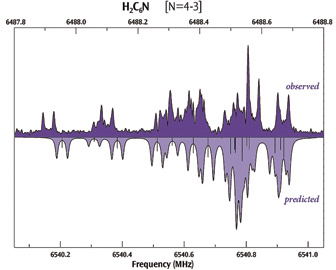
The plot below compares the observed (top) and computed (bottom) hyperfine spectra for H2C6N, showing very good agreement between the two.
Experimental data provided by S. E. Novick, W. Chen, M. C. McCarthy and P. Thaddeus.
Open shell species have particularly rich and complex spectra when studied with microwave spectroscopy. Such compounds are important in many contexts, including the chemistry of interstellar media. Researchers have studied the 1,1-difluoroprop-2-ynyl radical, F2CC=CH, a partially fluorinated variant of the propargyl radical. The combination of the observed microwave spectral data and calculation of various hyperfine tensors determined that the compound has a planar structure, a somewhat unexpected result.
The table below compares the values for several quantities from the theoretical calculation and derived from the experimental data, illustrating the very good agreement between the two.
| Constant | Calc. | Comb. Fit | Constant | Calc. | Comb. Fit |
|---|---|---|---|---|---|
| A0 | 11.108 | 11.126 | eaa | -43.236 | -43.674 |
| B0 | 3.926 | 3.927 | ebb | 20.852 | 16.159 |
| C0 | 2.901 | 2.904 | ecc | 2.158 | 0.359 |
| ?Nx103 | 0.44 | 0.57 | aF(H) | -43.226 | -32.542 |
| ?NKx103 | 17.0 | 19.1 | aF(H) | 97.52 | 145.73 |
| ?Kx103 | -1.5 | -30.0 | Taa(H) | 20.852 | 16.159 |
| dNx103 | 0.13 | 0.19 | Taa(F) | 97.52 | 145.73 |
| dKx103 | 9.6 | 14.6 | Tab(F) | 16.1 | 13.4 |
Calculation performed at UB3LYP/aug-cc-PVQZ. Combined fit IF=0,1.
Reference: L. Kang & S.E. Novick, J. Chem. Phys. 125 (2006) 054309.
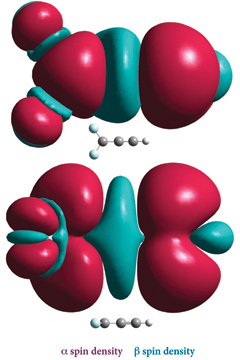
The plots at the right depict the spin density for 2CC=CH (with the a spin density in burgundy and the ß spin density in teal), situated perpendicular (top) and parallel to the plane of the molecule. Note the small amount of ß spin density on the H atom.
Explore
Explore Diverse Chemical Arenas
Gaussian's predictive powers are just as extensive in other chemical contexts as they are in spectroscopy.
Thermochemistry
Accurate predictions of ?G are vital to understanding many chemical reactions. Gaussian offers a variety of very accurate energy methods for predicting thermochemical quantities, including the Complete Basis Set (CBS) methods, the Gaussian-1 through Gaussian-4 method families, and the W1 methods. In addition to ?G and ?H, you can predict heats of formation, atomization energies, ionization potentials, electron affinities and proton affinities for a wide range of compounds at the highest available accuracy.
Photochemistry and other Excited State Processes
In addition to the spectroscopic features considered earlier, Gaussian also provides several other features for studying systems in their excited states. Using these capabilities, you can study the absorption properties of dyes and other chromophores, the photodecomposition rates of pesticides and other compounds, the properties of materials of potential use for solar energy, and many other equally important research problems.
Gaussian offers many methods for studying such reactions, suitable for systems of varying sizes, including the time-dependent DFT method, the EOM-CCSD method (comparable in accuracy and cost to coupled cluster singles and doubles ground state calculations), and the CASSCF method which provides a multireference description of molecular systems and can also be used to locate conical intersections on excited state-ground state potential energy surfaces.
Solvent Effects
Solvent Effects can be taken into account when optimizing structures and predicting most molecular properties. For example, the VCD investigation of the alanine peptide chain we considered on pages 4-5 was carried out in solution. In fact, in this case, the gas phase results are very different and solvent effects are crucial to studying this system. Gaussian's solvation capabilities are the most advanced available, and they provide roughly comparable performance to gas phase studies for many computation types.
What is Unique About Gaussian's ONIOM Capabilities?
Many programs now include some version of MO:MM models. However, Gaussian's ONIOM facility is far more advanced in many important ways:
- It is a general facility allowing you to use any method for any layer, supporting both MO:MM and MO:MO models. Gaussian's new implementations of semi-empirical methods including analytic frequencies are also available to ONIOM calculations. Two and three layer ONIOM calculations are supported by all features.
- ONIOM is an integral part of Gaussian. All molecular properties are supported for ONIOM calculations. Excited states and molecules and reactions in solution are supported in addition to ground state, gas phase systems.
- Energies, optimizations and efficient analytic frequencies are provided. Also, true IRC calculations can be performed (rather than mere "coordinate driving"). These capabilities allow you to characterize stationary points and explore potential energy surfaces even for very large molecules and with electronic embedding. Wavefunction stability testing and optimization are also supported.
- Different initial guesses can be specified for each ONIOM layer, including retrieving results from previous jobs.
- The implementation in Gaussian is efficient and reliable.
Complex Modeling
Complex Modeling, Yet Easy-to-Use Features
Gaussian is a powerful program offering sophisticated modeling capabilities. It is nevertheless very easy to use, even for new users. There are many ways that Gaussian makes studying molecules and reactions simple and straightforward. For example, its consistent and intuitive user input and carefully chosen default settings hide algorithmic and procedural complexity, allowing you to focus on the chemistry.
Automation
Gaussian also automates many compound calculation types whose steps traditionally have to be performed separately and explicitly:
- The quadratic synchronous transit (QST) approach automates transition structure optimization. You need simply provide the reactants, products and optionally a starting guess for the transition state.
- The high accuracy energy models in the CBS, Gaussian-1 through Gaussian-4, and W1 families consist of many diverse calculations whose results must be combined for the final energy value. Gaussian automates all of these methods and reports the final model energy.
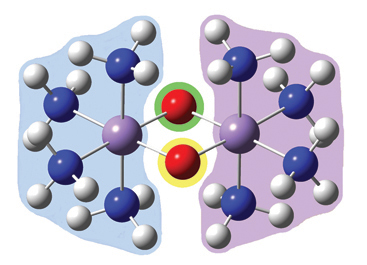
- Gaussian now provides a fragment guess capability which allows you to define fragments within the molecule whose separate initial guesses can be used to form the initial guess for the calculation. Previously, considerable effort was required to examine and reorder molecular orbitals in order to set up an appropriate initial guess for systems like antiferromagnetic transition metal complexes.
| Electronic state | ?E |
|---|---|
| Antiferromagnetic singlet | ground state |
| Spin multiplicity 11 | 4.4 kcal/mol |
| Open shell singlet | 60.2 kcal/mol |
| Closed Shell singlet | 154.5 kcal/mol |
- Gaussian provides the ability to test wavefunctions for instability and to automatically reoptimize non-ground state wavefunctions. This capability is very important for open shell systems, to ensure that the desired electronic state is in fact being modeled. We used it extensively in the study of the manganese complex described just previously.
Intuitive Presentation of Results
Gaussian presents results in as straightforward and comprehensible a manner as possible. First and foremost, the GaussView 5 graphical interface makes setting up jobs and examining results visually easy. In addition, Gaussian provides many convenience features which convey the computational outcome and the associated chemistry in forms which are familiar and recognizable to experimental researchers.
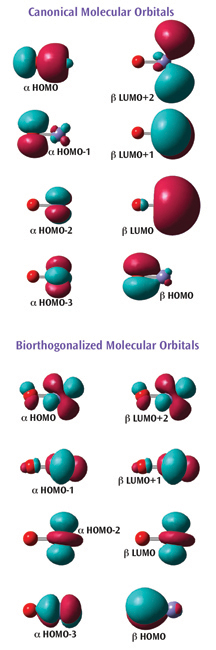
An example of the latter introduced in Gaussian is illustrated at the right. The figure shows two sets of orbitals for FeO+. This system is a quartet, and it is accordingly modeled using an unrestricted method.
The first set of orbitals (top) are the default canonical orbitals. They can be difficult to interpret for molecules like this one since they are spin polarized.
Understanding the bottom set of orbitals is much more straightforward. These orbitals have been biorthogonalized—transformed via an energy-invariant rotation—in order to produce the "corresponding orbitals." With this representation, it is clear that the molecule contains five singly occupied orbitals: four a unpaired electrons localized on the iron atom, and one ß unpaired electron localized on the oxygen atom.
Gaussian can also report the atomic contributions to the molecular orbitals. For example, the a HOMO in the canonical orbital set is composed of about 70% p-orbital on the oxygen and about 20% s-orbital on the iron.
Spin density itself can also be computed and visualized. We saw an example of this previously above.
Not all product information on our website is available in English and German, but our sales experts are happy to assist you in either language. Please schedule a consulation appointment via email at