Wolfram System Modeler - Elemente von Mathematica
Analyse und Design mit Mathematica
Die Analyse von Modellen des System Modelers kann mit Mathematica durchgeführt werden. Die Integration von Mathematica erlaubt die programmiertechnische Kontrolle von Simulationen, die mit dem System Modeler erstellt wurden, oder das Finden von Modellgleichgewichten mit integrierten Funktionen. Weiterhin können Modellkalibrierung und Systemoptimierungen unter Verwendung der symbolischen und numerischen Funktionen von Mathematica durchgeführt werden. Mit der Anbindung von Mathematica ist die Präsentation der Ergebnisse mit erweiterten Grafiken und zusätzlicher Interaktivität möglich.
Programmierbare Steuerung von Simulationen
Mit einer interaktiven Mathematica Notebook-Umgebung, die mit der Wolfram Language ausgestattet ist, haben Anwender die vollständige Kontrolle über die Simulationen. Dafür legen sie programmatisch Anfangsbedingungen, Parameterwerte und Eingangssignalfunktionen fest.
Durchläufe von Simulationen über Sätze von Parameterwerten, einschließlich Monte-Carlo-Simulationen, werden automatisch parallel ausgeführt. Anwender greifen auf erweiterte Simulationsoptionen zu, verwalten den Kompromiss zwischen Simulationsgeschwindigkeit und Simulationsdetails durch Auswahl eines der vielen verfügbaren Solver, ändern die Solver-Toleranz und Schrittgröße und vieles mehr.
Beispiele:
Aktive Dämpfung » | Hüpfende Bälle » | Insulinsignal »
Optimierung und Design
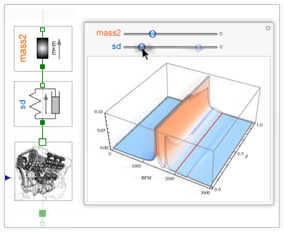
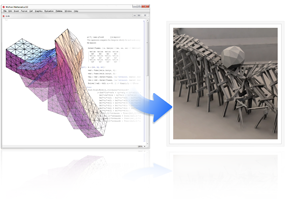
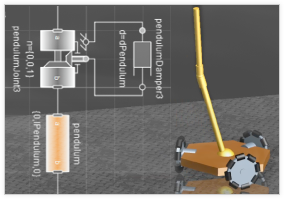
Mit Mathematica kann die Planung der Geometrie von dreidimensionalen mechanischen Systemen durchgeführt oder gleichungsbasierte eigene Komponenten erzeugt werden. Sobald ein Modell mit dem System Modeler zusammengebaut wurde, kann Mathematica dazu verwendet werden, optimale Modellparameter zu finden. Ebenso können eigene Benutzerumgebungen für die manuelle Untersuchung, numerische Versuche oder feinere Abstimmungen durchgeführt werden.
Beispiele:
Bagger » | Aktive Dämpfung »
Analyse von Modellen und Gleichungen
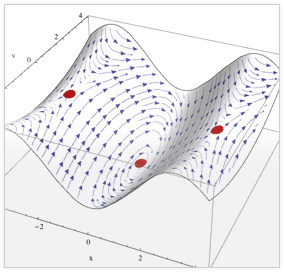
Anwender führen ihre eigenen symbolischen und numerischen Berechnungen durch, indem sie auf die vollständigen Modellgleichungen und Simulationsergebnisse ihrer Modelle zugreifen. Hierbei kann die volle Leistungsfähigkeit der Wolfram Language in ihre Modellanalyse eingebracht werden.
System Modeler-Simulationen können programmatisch gesteuert und integrierte Funktionen zum Finden von Modellgleichgewichten, zum Linearisieren von Modellen etc. verwendet werden. Anwender führen die Modellkalibrierung und Systemoptimierung mit den symbolischen und numerischen Funktionen von Mathematica durch und präsentieren ihre Ergebnisse mit fortschrittlichen Grafiken und Interaktivität. Die Umgebung der Wolfram Language ist so konzipiert, dass die Untersuchung und Analyse so effizient wie möglich ist. Durch die Eingabe von Befehlen in die Notebook-Umgebung wird automatisch eine Aufzeichnung ihrer Arbeit erstellt, die mit Kollegen geteilt oder für zukünftige Analysen wiederverwendet und verbessert werden kann. Notebooks kombinieren Code, Daten, erklärenden Text, Plots, Grafiken und interaktive Elemente in einem einzigen plattformunabhängigen Dokumentformat. Vorkonfigurierte Notebook-Vorlagen für Häufigkeits- und Empfindlichkeitsanalysen, Modellkalibrierungen und vieles mehr machen den sofortigen Einstieg leicht.
Beispiele:
Voll durchmischter Faulbehälter » | Aktive Dämpfung »
Entwurf von Regelsystemen
Mathematica enthält umfassende Features für Regelsysteme mit Stabilitäts- und Frequenzanalyse, Visualisierung und Reglerdesign. System Modeler-Modelle können automatisch so linearisiert werden, dass sie den Zustandsräumen für linear zeitinvariante Systeme in Mathematica entsprechen. Die Verwendung von numerischer Linearisation von Modellen oder die Beibehaltung benannter Parameter zur weiteren symbolischen Analyse sind ebenso möglich.
Beispiele:
LEGO Segway » | Satellit »
Volle Funktionalität von Mathematica
Die Modellgleichungen und Simulationsergebnisse des System Modelers sind von Mathematica aus vollständig zugänglich und können ohne weitere Bearbeitung oder Konvertierung mit den Algorithmen für symbolische oder numerische Mathematik weiterverwendet werden. Mathematica eignet sich mit seinen umfangreichen Statistikfunktionen, leistungsstarken Werkzeugen zur Datenanalyse, anpassbaren Grafiken und automatisch hinzugefügter Interaktivität hervorragend für die Modellanalyse.
Mehr:
Mathematica Features »
Modellkalibrierung
Freie Parameter werden durch Modellkalibrierung an Daten der realen Welt angepasst. Durch Simulationen des SystemModelers mit Mathematica können Parameterräume untersucht werden. Mit Hilfe der Optimierungsfunktionen von Mathematica werden die besten Anpassungswerte gefunden, die in den Modellen des SystemModelers weiterverwendet werden können.
Beispiele:
Wasserkocher »
Sensitivitätsanalyse
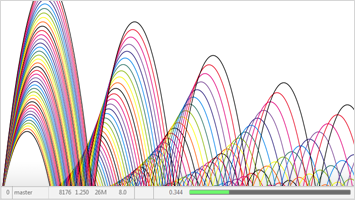
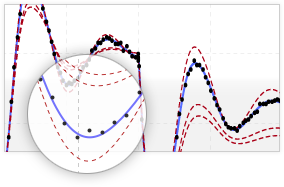
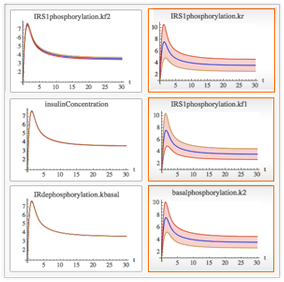
Modelle können simuliert und die Sensitivität von Systemvariablen unter Berücksichtigung festgelegter Parameter ermittelt werden. Das zeichnen von Sensitivitätsfrequenzbändern ist integriert. Mit der Integration von Mathematica lässt sich herausfinden, welche der relevanten Parameter leicht reagieren oder welche Parameter den größten Einfluss auf das Systemverhalten haben.
Beispiele:
Insulinsignal »
Grafische Darstellung und eigene Visualisierungen
Variablen und Empfindlichkeitsbereiche können direkt mit den Simulationsergebnissen grafisch dargestellt werden. Die Simulationsergebnisse des System Modelers werden in einem Standardformat für Interpolationsfunktionen ausgegeben und können direkt durch die Visualisierungsfunktionen von Mathematica genutzt werden. Eigene angepasste Grafiken, Animationen und Benutzeroberflächen sind ebenso möglich.
Beispiele:
Satellit » | Hüpfende Bälle »
Berechenbare Daten
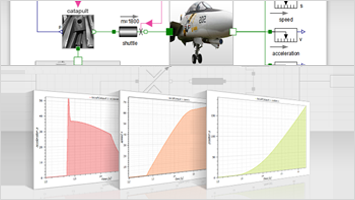
Modelica-Modell-Dateien sowie gespeicherte Simulationsergebnisse des System Modelers können direkt in Mathematica importiert werden. Neben dem Im- und Export der über hundert nativ von Mathematica unterstützten Datenformate können die Eingabedatenformate von Modelicas Standardbibliothekskomponenten genutzt werden. Durch die programmiertechnische Einbindung von Wolfram|Alphas umfangreicher Datensammlung zu Wetter, Erdbeben, Gezeiten und weiteren Fachgebieten werden Simulationen unter realistischen Bedingungen durchgeführt. Grafiken und Animationen können in den gängigsten Bild- und Multimediaformaten exportiert werden.
Beispiele:
Hausheizung » | Antriebssystem » | Wasserkocher »
Notebook-Umgebung
Die Mathematica-Umgebung wurde entworfen, um die Untersuchung und Analyse so effizient wie möglich zu gestalten. Jeder in ein Mathematica-Notebook eingegebene Befehl erzeugt automatisch einen Bericht, der mit Kollegen geteilt oder für zukünftige Verbesserungen genutzt werden kann. Notebooks kombinieren Quellcode, Daten, beschreibenden Text, Funktionsgraphen, Grafiken und interaktive Elemente in einem plattformunabhängigen Dokument im Computable Document Format (CDF).
Beispiele:
Hüpfende Bälle » | Aktive Dämpfung »