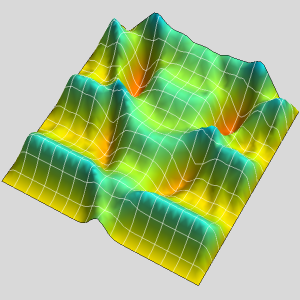
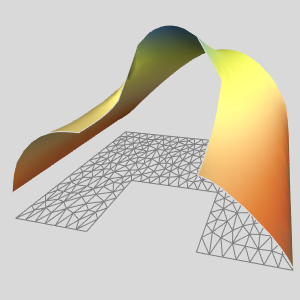
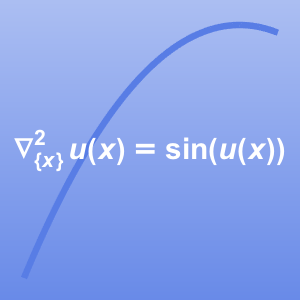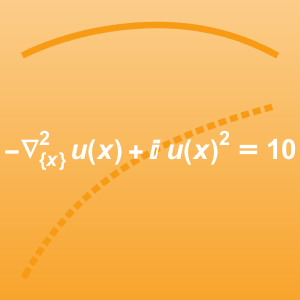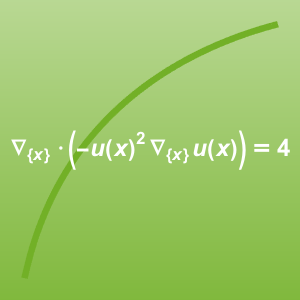Nichtlineare Finite Elemente
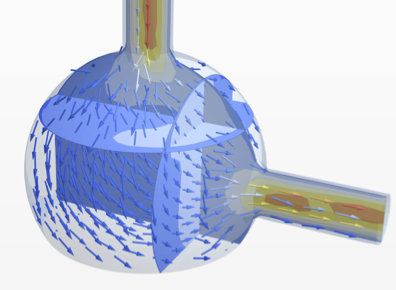
Mathematica 12 findet nun auch Lösungen für nichtlineare partielle Differentialgleichungen über beliebig geformten Regionen mit der Finiten-Elemente-Methode. Sind eine nichtlineare, wahrscheinlich gekoppelte partielle Differentialgleichung, eine Spezifikation einer Region und Randbedingungen gegeben, findet Mathematica Lösungen einer stationären und zeitabhängigen nichtlinearen partiellen Differentialgleichung. Diese Funktionalität ermöglicht es, bedeutend größere Klassen von industrie-relevanten Anwendungen aus Bereichen wie der Physik, Chemie, Mechanik, Strömungsdynamik und weiteren abzubilden.
- Unterstützung stationärer nichtlinearer partieller Differentialgleichungen über Regionen »
- Modellierung mit partiellen Differentialgleichungen abhängig von Raum, Zeit und der Abhängigkeitsvariablen »
- Verwendung partieller Differentialgleichungen abhängig von den Ableitungen der Abhängigkeitsvariablen »
- Lösen von komplexwertigen nichtlinearen partiellen Differentialgleichungen »
- Spezifikation nichtlinearer allgemeiner Neumann-Randbedingungen »
- Lösen zeitabhängiger nichtlinearer partieller Differentialgleichungen über Regionen »
- Transiente Problemstellungen nutzen automatische Zeitschrittverfahren
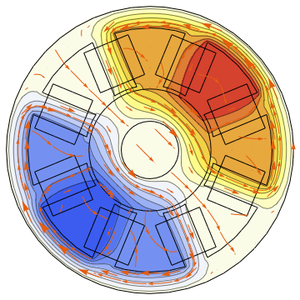
- Formulierung gekoppelter partieller Differentialgleichungen in der Multi-Physik-Analysis »
- Lösen rechnerischer Strömungsdynamikprobleme »
- Programmierung mit der Finiten-Elemente-Methode-Schnittstelle
- Verwenden des Newton-Algorithmus zum Finden von Wurzeln in großen Gleichungssystemen »