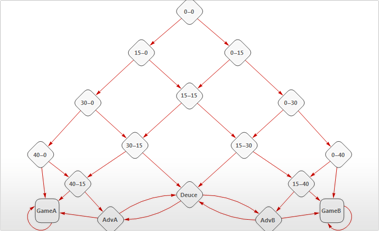
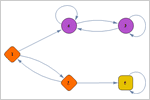
Markov-Ketten und Warteschlangen

Mathematica 9 bietet volle automatisierte Unterstützung für diskrete und stetige finite Markov Prozesse sowie für finite und infinite Warteschlangenprozesse und Warteschlangennetze mit Ankunfts- und Servicezeit-Verteilung. Die symbolische Darstellung dieser Prozesse in Mathematica machen es einfach allgemeine Prozesseigenschaften abzufragen, den Prozesse zu visualisieren, die Prozesspfade zu simulieren, Parameterschätzungen oder Wahrscheinlichkeitsuntersuchungen von Zeiträumen durchzuführen und die Anfangsverteilung sowie die Übergangswahrscheinlichkeiten zu berechnen. Die nahtlose Integration in Mathematica’s leistungsstarke symbolisch-numerische Berechnungsengine macht das Modellieren realitätsnaher Markov-Ketten und Warteschlangensysteme einfacher und flexibler als jemals zuvor.

Diskrete und stetige finite Markov-Prozesse.
Verwendung von Matrizen oder Graphen für die Spezifizierung der Markov Übergangswahrscheinlichkeiten.
Großer Umfang von strukturellen, transienten und limitierenden Eigenschaften für markov-Prozesse
Allgemeine Warteschlangenprozesse, einfache und mehrfache Stationen, finite und infinite Systemgröße
Unterstützung allgemeiner Anfangsverteilungen sowie Übergangswahrscheinlichkeiten (M/M, M/G, G/M, G/G, ...).
Volle Unterstützung von offenen (Jackson) oder geschlossenen (Gordon-Newell) Netzen von Warteschlangen.
Umfangreicher Support für Kennzahlen wie Wartezeiten
Markov –Prozesse und Warteschlangenprozesse werden umfänglich als Zufallsprozesse unterstützt.