Optimierung als Kernbestandteil der Wolfram Language
Für den Bereich der Optimierung steht in der Wolfram Language eine umfassende Sammlung von Werkzeugen bereit, um Modelle zu entwerfen, zu analysieren und auch mit geforderten Einschränkungen zu lösen. Die Optimierungsmethoden sind vollständig kompatibel mit anderen Kernbestandteilen der Wolfram Language wie beispielsweise maschinellem Lernen oder Statistik und können auch mit den integrierten, bereits für die Berechnung aufbereiteten Daten durchgeführt werden.
Optimierungsmodellierung
In der Wolfram Language können Ziele und Nebenbedingungen mittels mathematischer Funktionen, Ungleichheiten und Teilmengen modelliert werden. Ebenso lassen sich komplexe High-Level-Modelle auf einfache Weise mit Vektorvariablen, Vektorungleichheiten und geometrischen Regionen definieren. Die erstellten Modelle sind jederzeit wiederverwendbar, wenn sie programmatisch aus Daten, Diagrammen und anderen Objekten der Wolfram Language konstruiert wurden.
Leitfaden zur Optimierung »
Leitfaden zur konvexen Optimierung »
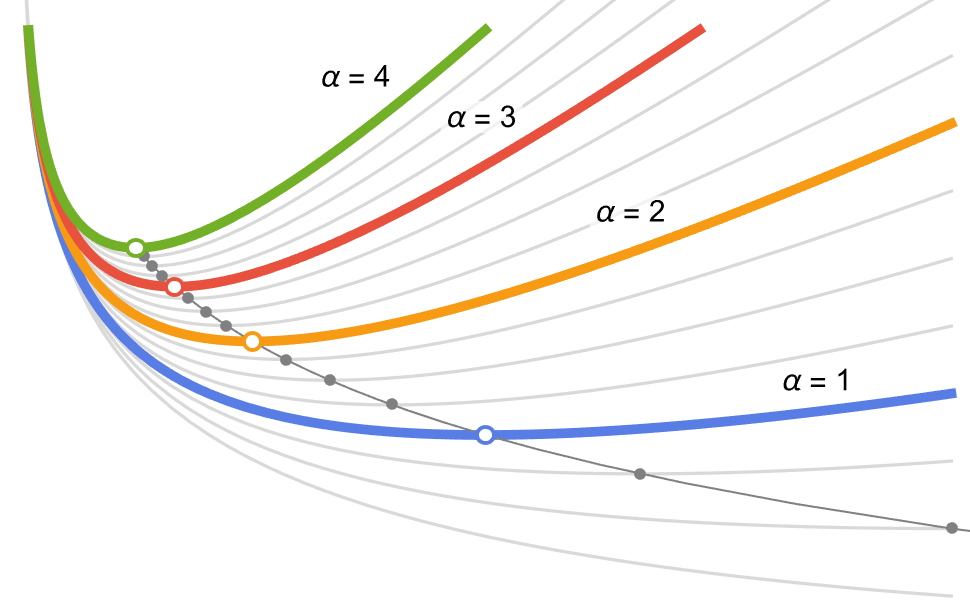
Lineare und konvexe Optimierung
Die Wolfram Language ist in der Lage, große konvexe Optimierungsaufgaben mit globalen, schnellen und zuverlässigen Methoden zu lösen. Die konvexe Optimierung umfasst wichtige Klassen wie die lineare, quadratische, semidefinite und konische Optimierung sowie Second-Order-Cone-Program (SOCP).
Der Befehl LinearOptimization »
Der Befehl QuadraticOptimization »
Leitfaden zur konvexen Optimierung »
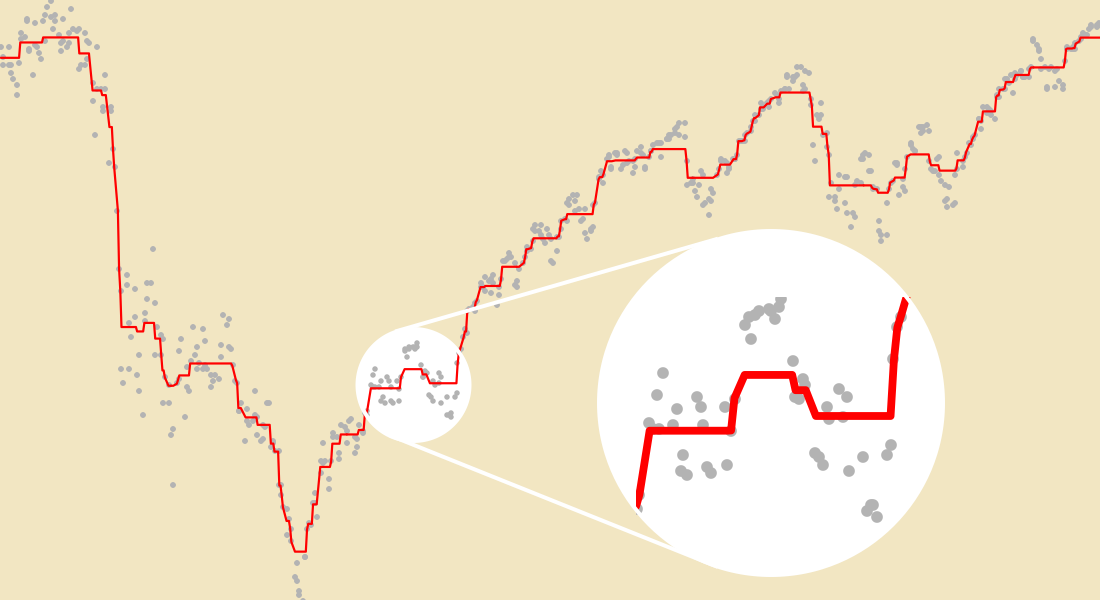
Lokale Optimierung
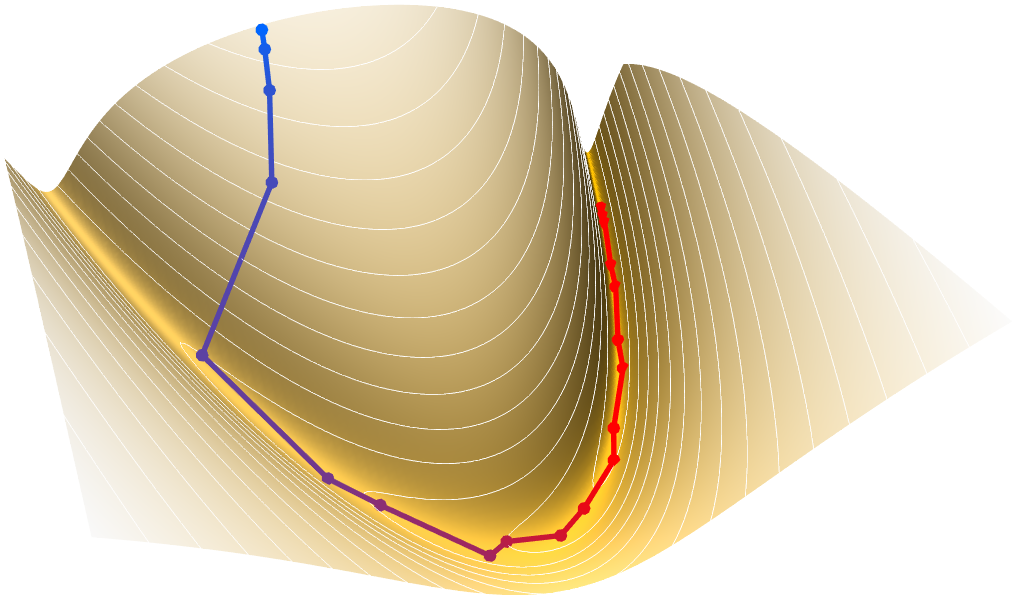
Lokale Optima mit oder ohne Nebenbedingungen lassen sich mittels der Wolfram Language einfach finden. Methoden für die lokale Optimierung sind schnell sowie skalierbar und reichen oft aus. Alternativ dienen sie zur Entwicklung komplexerer Methoden. Lokale Optimierungsaufgaben lassen sich mit Hilfe der automatischen Auswahl von Methoden, die vom Quasi-Newton- bis hin zum Innere-Punkte-Verfahren reichen, sowie mit der Berechnung von Ableitungen und der Kompilierung für größere Effizienz lösen.
Globale Optimierung
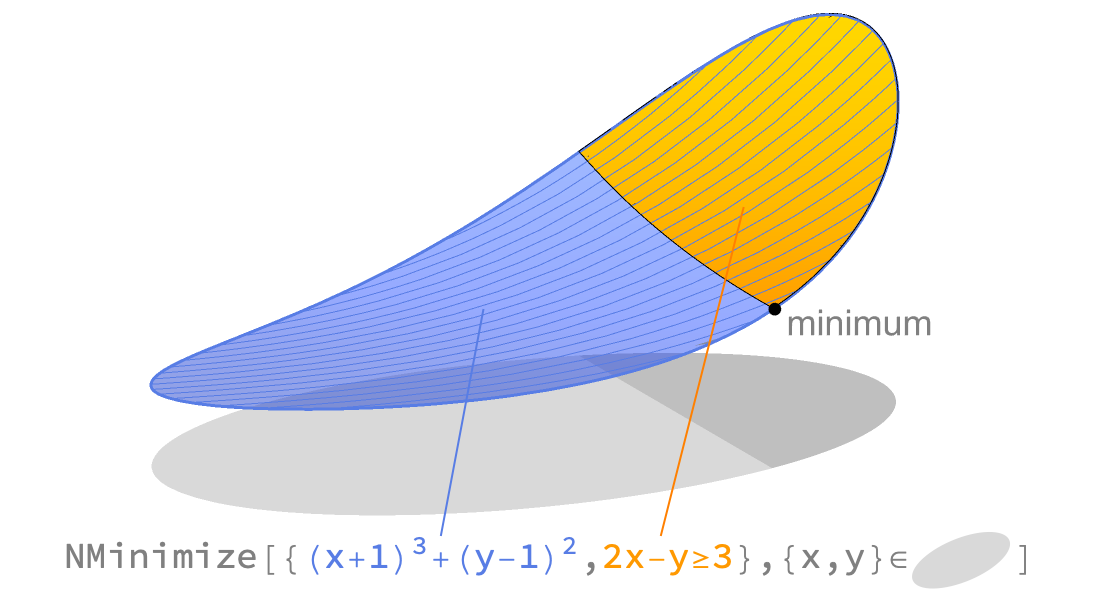
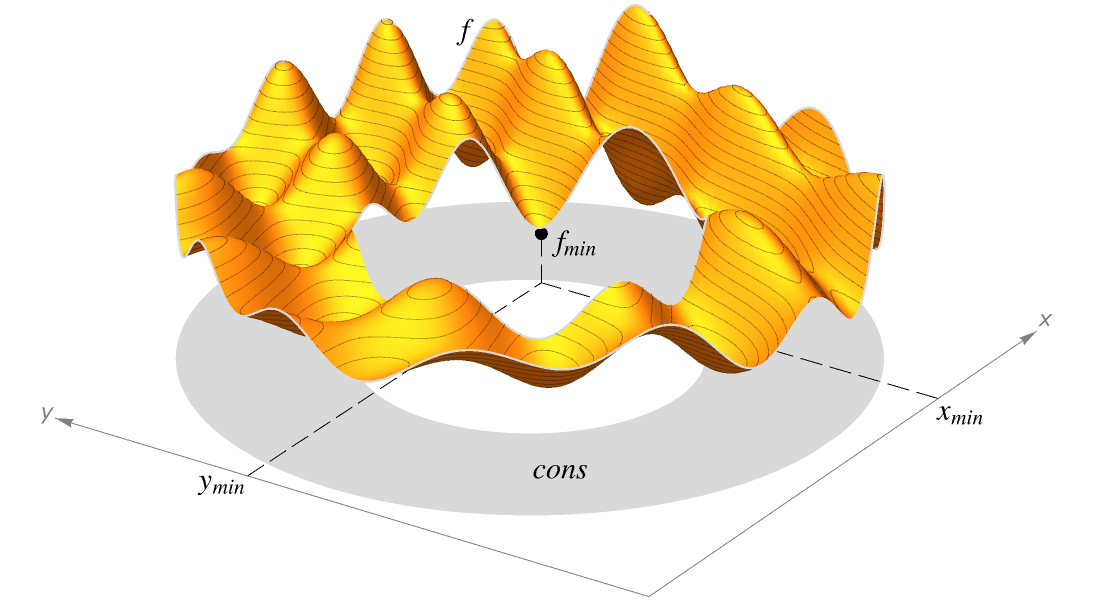
Die Aufgabe der globalen Optimierung besteht darin, das bestmögliche Ziel innerhalb der gegebenen Nebenbedingungen zu suchen. Die Wolfram Language bietet hierfür eine Vielzahl an Methoden, angefangen bei deterministischen Erweiterungen über die konvexe Optimierung bis hin zu stochastischen Verfahren.
Die Funktion NMinimize »
Die Funktion Minimize »
Leitfaden zur Optimierung »
Gemischt-ganzzahlige Optimierung
Die Wolfram Language unterstützt auch das Lösen konvexer Optimierungsprobleme, bei denen einige der Entscheidungsvariablen nur diskrete oder ganzzahlige Werte annehmen können. Dazu stehen Branch-and-Bound-, Cutting-Plane- und äußere Approximationsmethoden zur Verfügung.
Leitfaden zur konvexen Optimierung »
Beispiel für die Erstellung und Lösung von Sudoku-Spielen »
Parametrische Optimierung
Auch Optimierungsprobleme, die Parameter in Zielen und Nebenbedingungen verwenden, können mit der Wolfram Language gelöst werden. Dabei können viele Lösungen effizient mit Parameter Sweeps, sichere Lösungen für alle Werte (robuste Optimierung), erwartete Lösungen für zufällige Werte (stochastische Optimierung) oder die Sensitivität für Änderungen der Werte (parametrische Sensitivität) gefunden werden.
Die Funktion ParametricConvexOptimization »
Die Funktion RobustConvexOptimization »
Leitfaden zur konvexen Optimierung »
Symbolische Optimierung
Für die symbolische Optimierung erhält man mit der Wolfram Language Formeln für exakte globale Lösungen von Optimierungsproblemen. Lösungen in geschlossener Form sind verifiziert, wiederverwendbar und mit anderen Formeln kombinierbar. Dieselbe Modellierungssprache lässt sich mit exakten oder approximativ-numerischen Methoden verwenden.
Optimale Anpassung
Für die Modellanpassung als Brücke zwischen Modellen und Parametern lassen sich mit der Wolfram Language lineare und nichtlineare Anpassungsalgorithmen einsetzen, die Ziele wie kleinste Quadrate, kleinste absolute Abweichung, LASSO und Ridge-Regression verwenden.
Leitfaden zur statistischen Modellanalyse »
Leitfaden zur Kurvenanpassung »
Maschinelles Lernen »
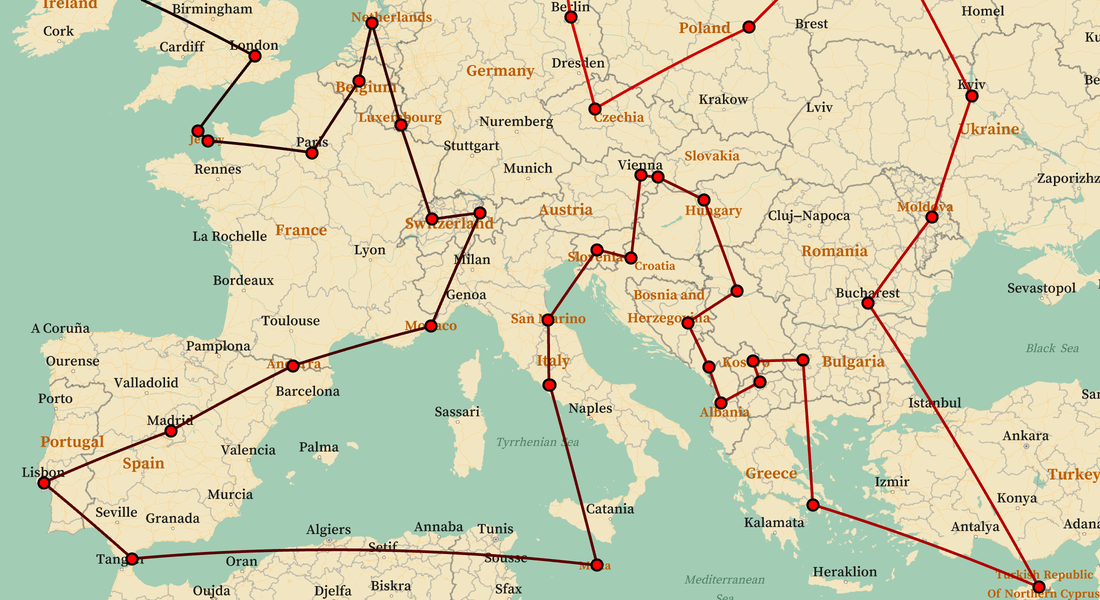
Optimierung in Spezialfällen
Die Wolfram Language stellt intuitive Schnittstellen bereit, um Aufgaben wie das Training neuronaler Netze, das Travelling-Salesman- oder Rucksackproblem oder andere spezielle Optimierungsaufgaben zu lösen.
Optimierungs-Partner
Die kommerziellen Solver von Gurobi, MOSEK und FICO Xpress können mit der Wolfram Language genutzt werden. Die Optimierungsfunktionen können automatisch Methoden verwenden, für die eine gültige Lizenz vorliegt.
Die Optimierung mit Gurobi »
Die Optimierung mit MOSEK »
Die Optimierung mit Xpress »
Wolfram Solutions
Nächste Schulungen
| Mathematica - Grundlagen und Programmiertechniken 02.02. - 05.02.2026 - Online |
| Modul: Einführung in Mathematica 13.04.2026 - Online |
| Modul: CDF-Programmierung mit Mathematica 13.04.2026 - Online |
Nächste Webinare
| Wolfram-Webinar: Power up your Plots 29.01.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Schnelleinstieg in die Wolfram Language und den System Modeler 19.02.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Neuronale Netze mit Mathematica - Konstruktion & Anwendung 05.03.2026 : 11:00 - 11:45 Uhr |
Buchen Sie Ihren Termin mit unseren Spezialisten
| Name | Produkt | Themen | |
|---|---|---|---|
 |
Harald Farcas | Wolfram Mathematica, Wolfram Finance Platform, System Modeler, Wolfram Cloud Produkte und Origin/OriginPro | Industrie, Behörden, akademische Kunden, Product Manager Wolfram, Schulungen und Produktvorstellung |
 |
Ralf Rosenberger | Origin/OriginPro, Mathematica, Minitab | Produktapplikation, professioneller Service, Beratung, Rahmenvereinbarungen |
 |
Andreas Heilemann | Mathematica, Minitab, OriginPro | Enterprise Business, Großkunden, Senior Key-Account-Manager |