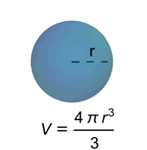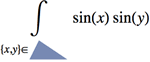4981

Einfache und formelbasierte Regionen

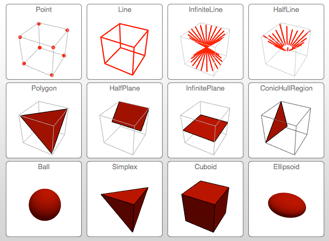
Einfache und formelbasierte Regionen in Mathematica 10

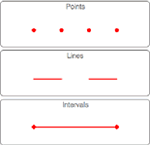
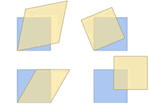
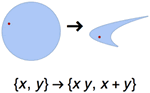
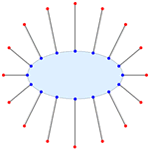
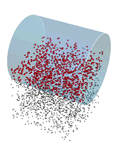
Mathematica Version 10 werden sowohl einfache als auch formelbasierte geometrische Regionen unterstützt. Im Gegensatz zu einfachen geometrischen Regionen, die häufig auftreten und einfach zu definieren sind, haben formelbasierte Regionen eine große beschreibende Wirkung und sind flexibel. Beide Arten von geometrischen Regionen können zur Berechnung von exakten oder angenährten Lösungen herangezogen werden, wobei Ergebnisse auch Parameter beliebiger Dimension enthalten können. Sowohl die einfachen als auch die formelbasierten Regionen unterstützen das Framework für geometrische Regionen, das die Berechnung von Eigenschaften (Fläche, nächster Punkt, usw.), Eingabe für weitere Berechnungen (Optimierungsaufgaben, Lösung partieller Differentialgleichungen, usw.) und Diskretisierung beinhaltet.

  • Die meisten bestehenden 2D- und 3D-Grafikprimitiven sind einfache Regionen.
  • Seite-Seite-Seite-, Seite-Winkel-Seite-Dreiecke usw.. »
  • Gerade, Strahl. »
  • Unendliche und halb-unendliche Ebene. »
  • Unendlicher und halb-endlicher linearer Kegel. »
  • Parallelogramm und allgemeine Parallelfläche.
  • Polyeder wie Tetraeder, Hexaeder, Prisma und Pyramide.
  • Einheitskugel in jeder Dimension. »
  • Umkugel in allen Dimensionen durch Punkte spezifiziert. »
  • Ellipsoide in allen Dimensionen und Orientierungen. »
  • Simplexe in allen Dimensionen und für alle Objekte einer Dimension. »
  • Implizite durch Ungleichungen und Gleichung spezifizierten Regionen. »
  • Parametrische durch Parameterfunktionen spezifizierte Regionen. »
  • Boolesche Kombinationen und Transformationen. »
  • Berechnung von Eigenschaften für alle Regionen wie beispielsweise Test auf Zugehörigkeit, kleinste Entfernung, nächster Punkt, Maßeinheiten (Länge, Fläche, Volumen), Zentroid usw. »
  • Symbolische und nummerische Integration von Flächen.
  • Symbolische und nummerische Optimierung von Flächen.
  • Symbolische und nummerische Lösung von Gleichungen mit Regionsbeschränkungen.
  • Nummerische Berechnung von partiellen Differentialgleichungen bei Regionen.
  • Diskretisierung in netzbasierte Regionen in 1D, 2D und 3D.

Basic Geometric Regions in 1D »
Basic Geometric Regions in 2D »
Basic Geometric Regions in 3D »
Basic Geometric Regions in nD »

Implicitly Defined Curves in 2D »
Parametrically Defined Curves in 2D »
Implicitly Defined Regions in 2D »
Formula Regions in 3D »

Boolean Regions »
Affine Transformation of a Region »
Nonlinear Transformation of a Region »
Cartesian Products of Regions »

Region Measures (Length, Area, Volume, etc.) »
Compute Region Centroids »
Integrate over Regions »
Compute Region Bounds »

Region Measures (Length, Area, Volume, etc.) »
Compute Region Centroids »
Integrate over Regions »
Solve PDEs over a Region »

Optimize over Regions »
Minimum Distance between Two Regions »
Curve Intersection »
Surface Intersection »

Find Formulas for n Dimensions »
Find Probabilities over Regions »
Formula Region Projections »
Create Discretized Regions »