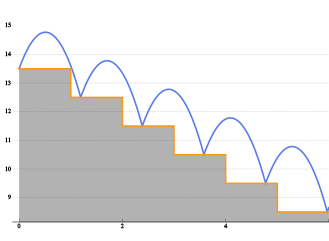
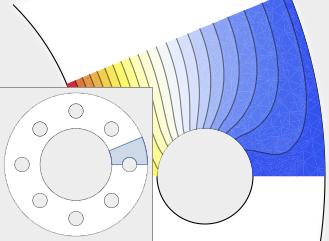
Lösung von Differentialgleichungen
Symbolisch retardierte & hybride Differentialgleichungen »
Mathematica 10 bietet viele weitreichende Verbesserungen für symbolische Berechnungen. Mit Version 10 können nun sogar symbolische Lösungen für hybride Differentialgleichungen (HDE) mit Ereignissen und Retadierende Differentialgleichungen (DDE) berechnet werden. Alle diskreten Rechenoperationen wurden durch neu entwickelte Algorithmen mit Methoden aus der Wahrscheinlichkeitsrechnung und Statistik erweitert. Neue Befehle für Kurvengeometrie sowie neu hinzugefügte Spezialfunktionen automatisieren viele Aufgaben. Insgesamt erleichtern die neuen Erweiterungen die Arbeit an vielen Anwendungen auf Hochschulniveau oder auch auf Forschungsebene. |
Partielle Differentialgleichungen »
Die Funktionen zum Lösen numerischer Differentialgleichungen wurden in Mathematica 10 so erweitert, dass jetzt die Finite-Elemente-Methode unterstützt wird. Der Lösungsprozess der Finiten-Elemente-Methode, inklusive Gitter und Elementgenerierung, ist vollständig automatisiert, wenn eine partielle Differentialgleichung, ein Definitionsbereich und entsprechende Randbedingungen gegeben sind. Stationäre und transiente Lösungen einer einzelnen partiellen Differentialgleichung oder eines Systems von partiellen Differentialgleichung lassen sich bis zur dritten Dimension lösen. |