Constrained Maximum Likelihood
Description
CML solves the general maximum likelihood problem subject to general constraints on the parameters - linear or nonlinear, equality or inequality.
Key Features
- Fast Procedures: fastCML, fastCMLBoot, fastCMLBayes, fastCMLProfile, fastCMLPflClimits
- New "Kiss-Monster" random numbers used in the bootstrap and random line search procedures
- Multiple Point Numerical Gradients
- Grid Search Method
- Trust Region Method
Major Features of CML
- fastCML, fastCMLBoot, fastCMLBayes, fastCMLProfile, and fastCMLPflClimits can speed convergence times from 10 to 180 percent over earlier versions of CML, depending on the type of problem.
- CML includes built-in models for estimating numerous limited dependent variable models, including exponential, exponential gamma, and Pareto duration models with or without censoring, Poisson, truncated Poisson, hurdle Poisson, seemingly unrelated regression Poisson, and latent variable Poisson models.
CML uses the Sequential Quadratic Programming method in combination with several descent methods selectable by the user - Newton-Raphson, quasi-Newton (i.e, DFP and BFGS), scaled quasi-Newton, and BHHH. There are also several selectable line search methods. A Trust Region method is also available which prevents saddle point solutions. Gradients can be user-provided or numerically calculated.
CML provides for statistical inference for constrained statistical models. Confidence limits may be computed from selected methods. Choices include:
- Newton-Raphson
- quasi-Newton (DFP and BFGS)
- scaled quasi-Newton
- BHHH
- PCRG
- steepest descent
- Confidence limits may be computed using bootstrap or Bayesian methods (using a weighted likelihood bootstrap) or by inverting Wald or likelihood ratio statistics. Confidence limits from inverting the likelihood ratio statistic are profile likelihood confidence limits.
- A trust region method constrains the direction at each iteration to an interval. This prevents poor starting values from pushing current estimates into far off regions. It also aids in resisting convergence at saddle points.
- A grid search method keeps CML working when it would otherwise halt without convergence. In most cases convergence is eventually achieved.
- Gradients can be numerically calculated or provided by the user. Accuracy is considerably improved by adding points to the usual numerical gradient calculation. Greater accuracy is gained by adding more points.
- The bootstrap and Bayesian procedures and the random line search algorithm implement the new "Kiss-Monster" random number generator introduced in GAUSS 3.6. This generator has a period of approximately 10^8859, long enough for any serious Monte Carlo work.
Several examples are included with CML, including tobit, nonlinear curve fitting, simultaneous equations, nonlinear simultaneous equations, and factor analysis models.
Example
CML is especially suited for models with complex constraints on parameters. The GARCH model, for example, requires a number of inequality constraints to ensure the stationarity of the model. Because CML provides for general nonlinear constraints, it is possible to enforce any type of constraint. The GARCH model requires a number of inequality constraints to ensure the stationarity of the model.
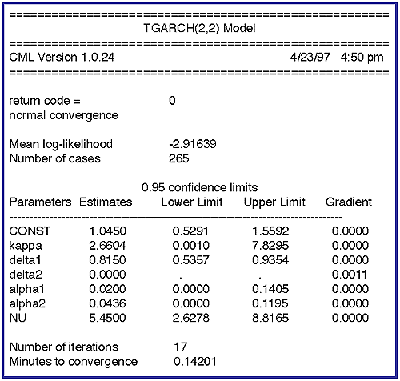
In the first example, a TGARCH(2,2) model is estimated where the residuals are assumed to have a Student's t distribution in order to measure the "fatness" or platykurtosis of the tails of the observed distribution of a well-known stock index measured monthly. The "NU" parameter, the "degrees of freedom" parameter in the t distribution, must be greater than 2, but the extent to which it is greater than 2 indicates the amount of platykurtosis. In this case, the index is clearly lplatykurtotic.
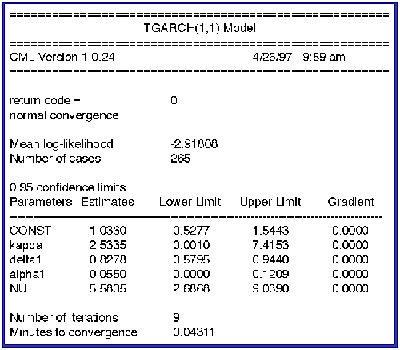
The "delta2" parameter is on the constraint floor. A Lagrange multiplier is available for testing the constraint, which in this case is the same as the gradient and is equal to .0011. This, plus the fact that the lower confidence limits of the "alpha" parameters are on the constraint boundary, suggest that a TGARCH(1,1) model might be a better model. The following are the estimates for the TGARCH(1,1) model:
The likelihood ratio test of the TGARCH(2,2) model over the TGARCH(1,1) model is .4478 (=265*(2.91808-2.91639)) which is not statistically significant. The likelihood ratio of the TGARCH(1,1) over the GARCH(1,1) model, in which the errors are assumed to have a Normal distribution, is 9.9665 with 1 degree of freedom. We thus accept the TGARCH(1,1) model under the rule of parsimony over both the TGARCH(2,2) and GARCH(1,1) models.
The likelihood ratio statistic for the GARCH(1,1) model over an ordinary least squares model is 75.2043 with 4 degrees of freedom which is highly significant and is strong evidence for the GARCH specification of the stock index.
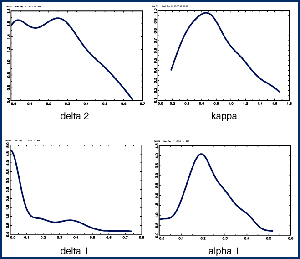
Here are kernel density plots of the distribution of the coefficients of the GARCH(1,1) model from a bootstrap:
CML provides for a variety of methods for statistical inference. Among them are the usual standard errors and t-statistics, confidence limits by inversion of the Wald statistic or the likelihood ratio statistic, Bayesian limits by the method of weighted likelihood bootstrap, as well as the usual bootstrap method.
Platform: Windows, LINUX and UNIX.
Requirements: GAUSS/GAUSS Light 3.6.23 or greater.