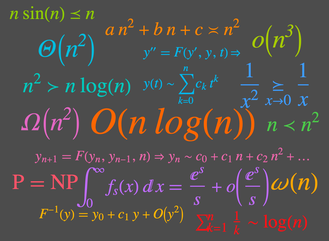Symbolische & Numerische Berechnung
Asymptoten
Mathematica 12 führt vollständig automatisierte asymptotische Berechnungen ein, die leicht einzusetzen sind. Asymptotische Methoden stellen - neben exakten symbolischen und nährungsweisen numerischen Berechnungen - eine weitere Berechnungsart für Analysis und Algebra dar. Dabei werden asymptotische Methoden häufig dann eingesetzt, wenn außergewöhnlich hartnäckige Aufgabenstellungen vorliegen. Zudem sind sie in den verschiedensten Fachrichtungen wie Zahlentheorie, Algorithmusanalyse, Statistik, theoretische Physik und numerische Methoden einsetzbar.
Analysis
Die Analysisfunktionen der Wolfram Language sind bereits weit entwickelt, wurden aber mit Mathematica 12 nochmals erheblich verbessert. Neue Analysisbereiche wurden automatisiert, bereits bestehende Funktionen verbessert und das komplette Subsystem neu strukturiert, um eine bessere Erlern- und Anwendbarkeit zu erreichen. Obwohl die Analysis als ein ausgereiftes Fachgebiet scheint, wird sie weltweit von immer mehr und vor allem immer jüngeren Personen eingesetzt, da die mächtigen Modelle in einer ständig wachsenden Anzahl von Disziplinen eingesetzt werden können.
Algebraische Berechnungen
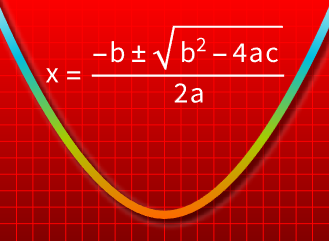
Mathematica 12 erweitert seine bereits leistungsstarken Möglichkeiten in der algebraischen Berechnung um Funktionen für Benutzer auf jedem Wissensniveau, angefangen bei Schülern bis hin zu Forschern. Die Verbesserungen reichen von neuen Funktionen, die Gleichungen Schritt für Schritt bearbeiten, über leistungsfähigere Gleichungs- und Optimierungssolver bis hin zum Nachweis von Gleichungssätzen.
Konvexe Optimierung
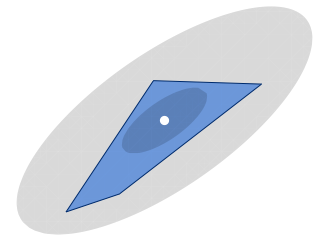
Mathematica Version 12 erweitert die Bandbreite an Optimierungsverfahren, um das Finden von Lösungen für konvexe Funktionen mit konvexen Bedingungen einzuschließen. Für die damit beschreibbaren konvexe Optimierungsprobleme sind schnelle und robuste Algorithmen sowohl in Theorie als auch Praxis vorhanden. Die mit den Neuerungen in Mathematica 12 lösbaren konvexen Optimierungsmodelle werden in immer mehr Bereichen wie beispielsweise Statistik, Finanzen, Signalverarbeitung und Geometrie klassifiziert.
Nichtlineare Finite Elemente
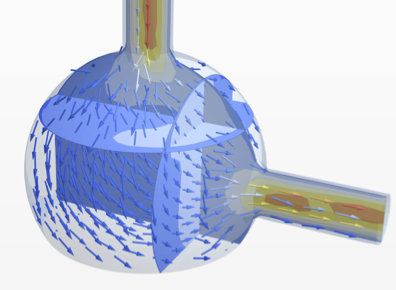
Mathematica 12 findet nun auch Lösungen für nichtlineare partielle Differentialgleichungen über beliebig geformten Regionen mit der Finiten-Elemente-Methode. Sind eine nichtlineare, wahrscheinlich gekoppelte partielle Differentialgleichung, eine Spezifikation einer Region und Randbedingungen gegeben, findet Mathematica Lösungen einer stationären und zeitabhängigen nichtlinearen partiellen Differentialgleichung. Diese Funktionalität ermöglicht es, bedeutend größere Klassen von industrie-relevanten Anwendungen aus Bereichen wie der Physik, Chemie, Mechanik, Strömungsdynamik und weiteren abzubilden.