Zuverlässigkeitsanalyse
Mathematica 9 ergänzt umfassende Funktionen für Zuverlässigkeitsanalyse zu den bereits vorhandenen mächtigen stochastischen und statistischen Methoden. Alle Verfahren wie Folgen, Parallelformen, konsekutive und allgemeinere k-aus-n-Methoden können mit symbolischen und numerischen analysiert werden. Warm, Cold, und Mixed Standby Systeme werden unterstützt. Eine breite Palette von Importance Measures hilft dabei, zielgenau die wichtigsten Subsysteme zu identifizieren und die Reliabilität des Systems zu erhöhen. Die Methoden der Lebendaueranalyse bieten Komponentenmodelle aus zensierten Daten wie sie typischerweise bei Feldtesten oder beschleunigten Lebendauertests auftreten.
- Alle wichtigen parametrischen Lebensdaueranalyseverteilungen (Exponential, Weibull, Erlang, Hypoexponential, ...).
- Unterstützung nichtparametrischer und abgeleiteter Lebensdaueranalyseverteilungen
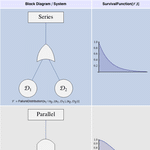
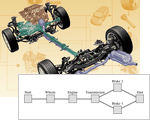
- Unterstützung für Folgen, Parallelformen, konsekutive und allgemeinere k-aus-n-Strukturen.
- Reliability block diagram-based system models.
- Fehlerbaum-basierte Modelle
- Vollständige Unterstützung von Standby Systemmodellen wie Cold, Warm, und Mixed Standby Systemen mit vollständigem oder unvollständigem Switching.
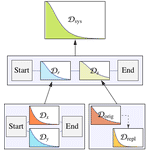
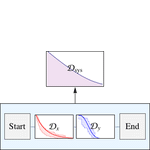
- Unterstützung für hierarchisches Modellieren von Zuverlässigkeitssystemen unter Zuhilfenahme von Blockdiagrammen, Fehlerbäumen und Standby Systems verschiedener Zustände.
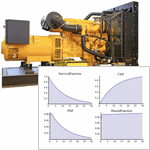
- Symbolische und numerische Berechnung von Eigenschaften wie Zuverlässigkeitsfunktion, Hazard Rate oder mittlerer Ausfallabstand (MTTF).
- Einfaches Simulieren jedes Systems
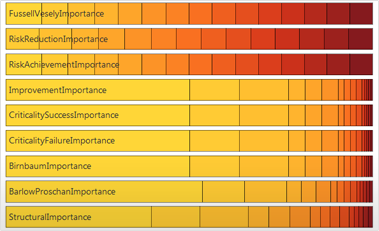
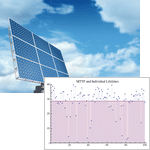
- Volle Unterstützung von Importance Measures wie Birnbaum u.a.
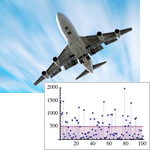
- Breite Palette von Methoden der Lebensdaueranalyse, einschließlich Schätzen von zensierten Daten und proportionalem Hazard Modeling