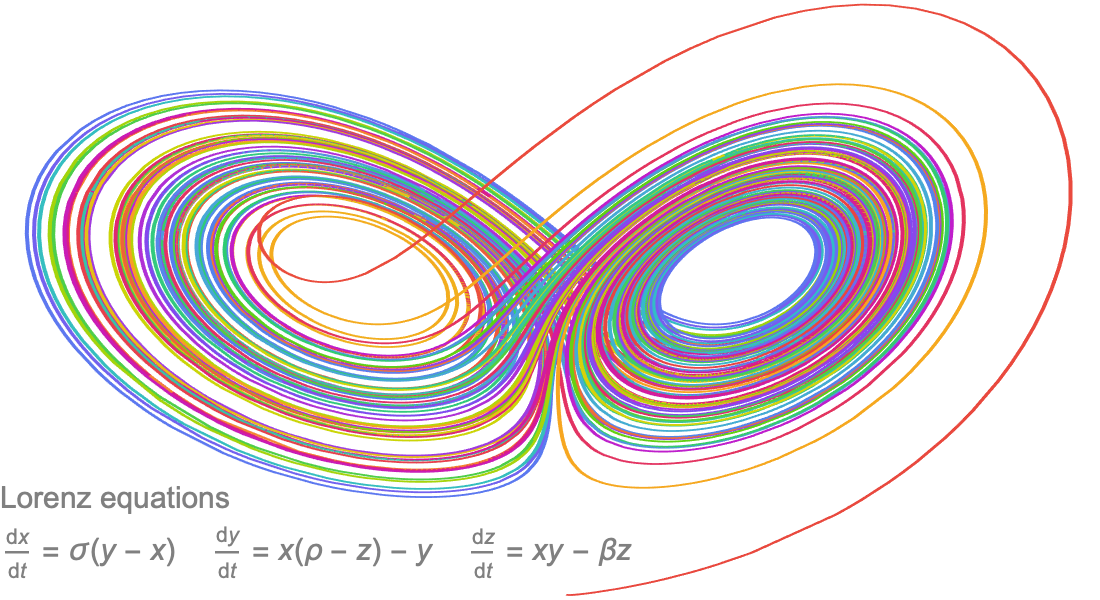Infinitesimalrechnung & Algebra als Kernbestandteil der Wolfram Language
Mit der Wolfram Language lassen sich sowohl symbolische als auch numerische mathematische Berechnungen durchführen. Damit eignet sich die Wolfram Language für alle Schwierigkeitsstufen - angefangen bei der Schulmathematik auf Mittelstufenniveau bis hin zu fortgeschrittenen Mathematikaufgaben aus der Forschung. Die leistungsstarken Berechnungsfunktionen der Wolfram Language lassen sich dabei mit fortschrittlichen Visualisierungsmöglichkeiten und sofort berechenbaren integrierten Daten kombinieren.
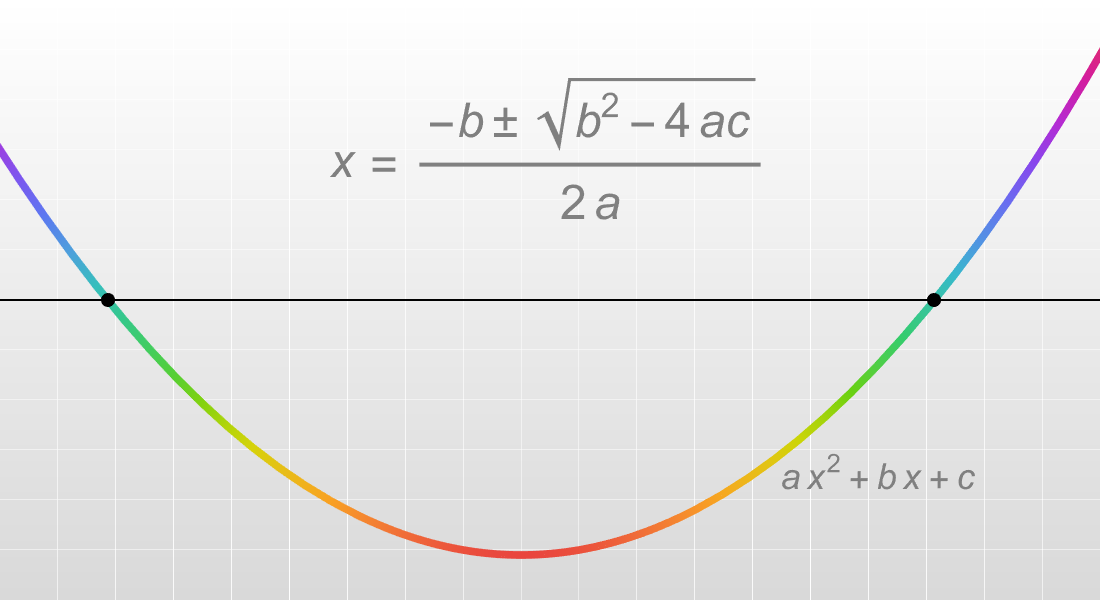
Elementare und polynomiale Algebra
Neben dem Faktorisieren und Expandieren von Polynomen können mit der Wolfram Language Gleichungen sowie Ungleichungen bearbeitet, kombiniert und vereinfacht werden. Gleichungssysteme lassen sich exakt oder mit beliebiger numerischer Genauigkeit lösen. Schritt-für-Schritt-Operationen unterstützen Anwender beim Verständnis von Grundlagen, während fortgeschrittene Algorithmen komplexe Gleichungen lösen.
Leitfaden zur Formelbearbeitung »
Leitfaden zur Polynomalgebra »
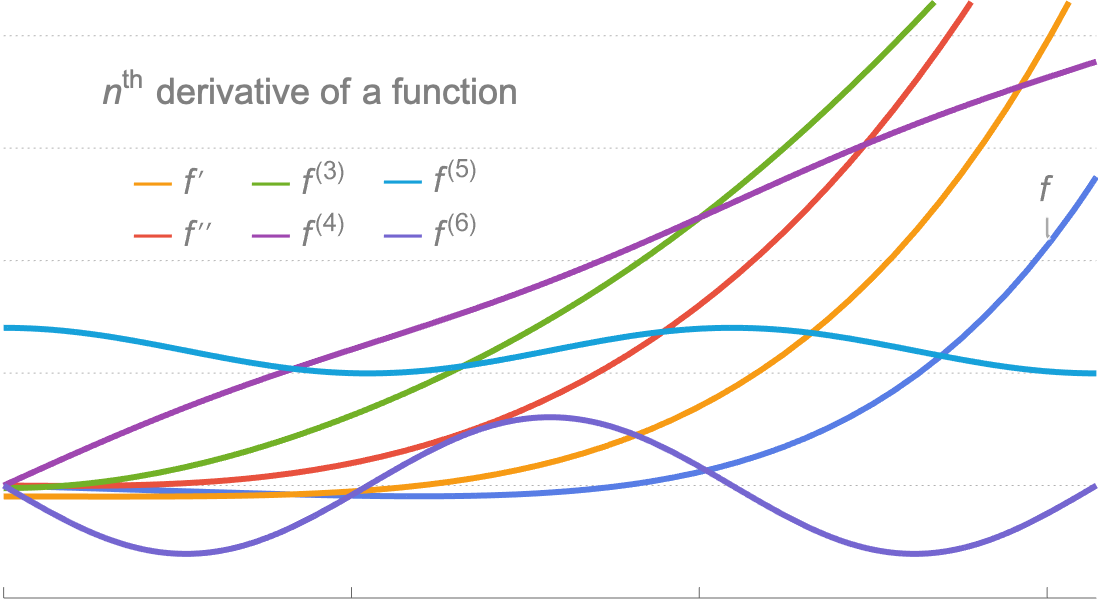
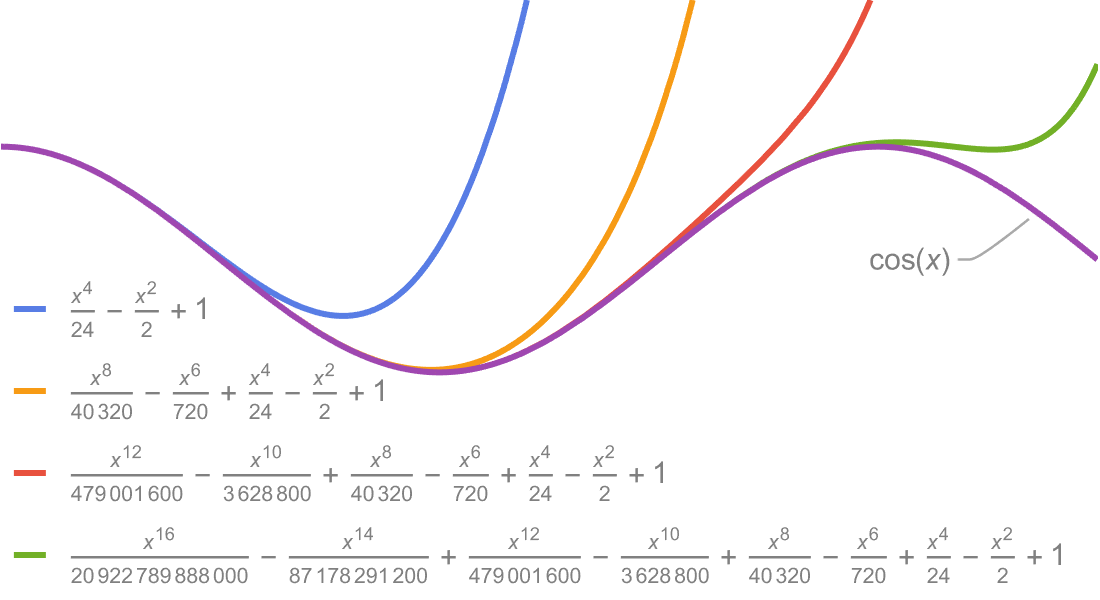
Infinitesimalrechnung
Im Bereich Infinitesimalrechnung können mit der Wolfram Language Grenzwerte, Ableitungen, Integrale und weitere Konzepte mittels einer Kombination aus leistungsstarken symbolischen und numerischen Methoden berechnet werden, um optimale Ergebnisse zu erhalten.
Leitfaden zur Infinitesimalrechnung »
Leitfaden zu Funktionseigenschaften »
Interaktiver Kurs zur Infinitesimalrechnung »
Differentialgleichungen
Mit der Wolfram Language lassen sich gewöhnliche, partielle, verzögerte, integrale und hybride Differentialgleichungen lösen, um damit beispielsweise das Verhalten von Systemen vorherzusagen oder die Abhängigkeit von Parametern zu verstehen.
Leitfaden zu Differentialgleichungen »
Leitfaden zum Modellieren partieller Differentialgleichungen »
Interaktiver Kurs zu Differentialgleichungen »
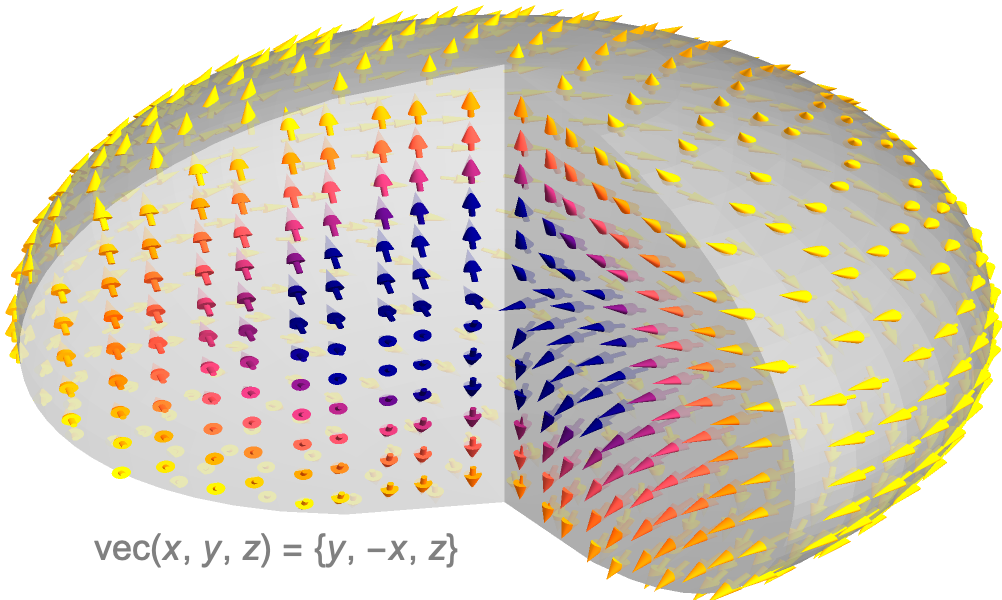
Multivariate Berechnungen und Vektorrechnung
Die Wolfram Language erlaubt es, zentrale Konzepte der Bereiche Geometrie, partielle Differentialgleichungen, Physik und verwandten Gebieten zu erforschen. Dabei können einfache Berechnungen von mehrdimensionalen skalaren oder vektoriellen Grenzwerten, partielle, Gradient-, Divergenz- und weitere Ableitungen sowie Integrale, wie beispielsweise Linien-, Flächen- oder Volumenintegrale berechnet werden. Berechnete Vektorfelder sowie deren Lösungen können visualisiert werden.
Leitfaden zu Vektoroperationen »
Leitfaden zur Vektoranalyse »
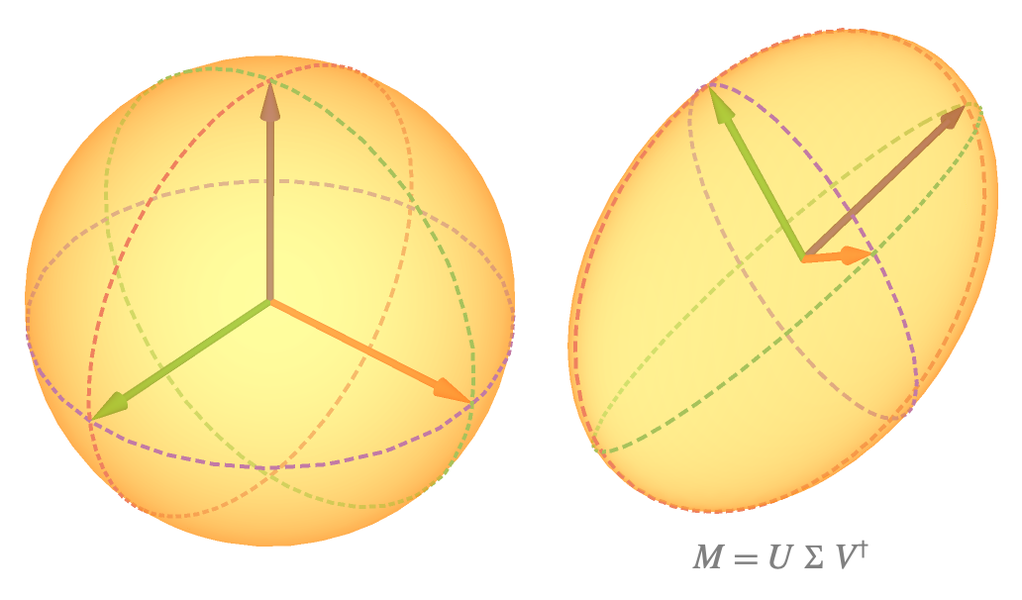
Lineare Algebra
Die vollständige Palette an Funktionen für die lineare Algebra, die in der Wolfram Language für Anwender zur Verfügung steht, umfasst u. a. sowohl numerische als auch symbolische dichte, spärliche und strukturierte Methoden, die wiederum häufig in der Datenwissenschaft, Statistik, Optimierung und Geometrie zum Einsatz kommen. Des Weiteren unterstützt die Wolfram Language das automatische Lösen linearer Systeme, die Berechnung von Matrix-Eigenkompositionen sowie das Analysieren von Daten mit Singulärwertzerlegung.
Leitfaden zu Matrizen und Linearer Algebra »
Leitfaden zu Matrixoperationen »
Interaktiver Kurs zur linearen Algebra »
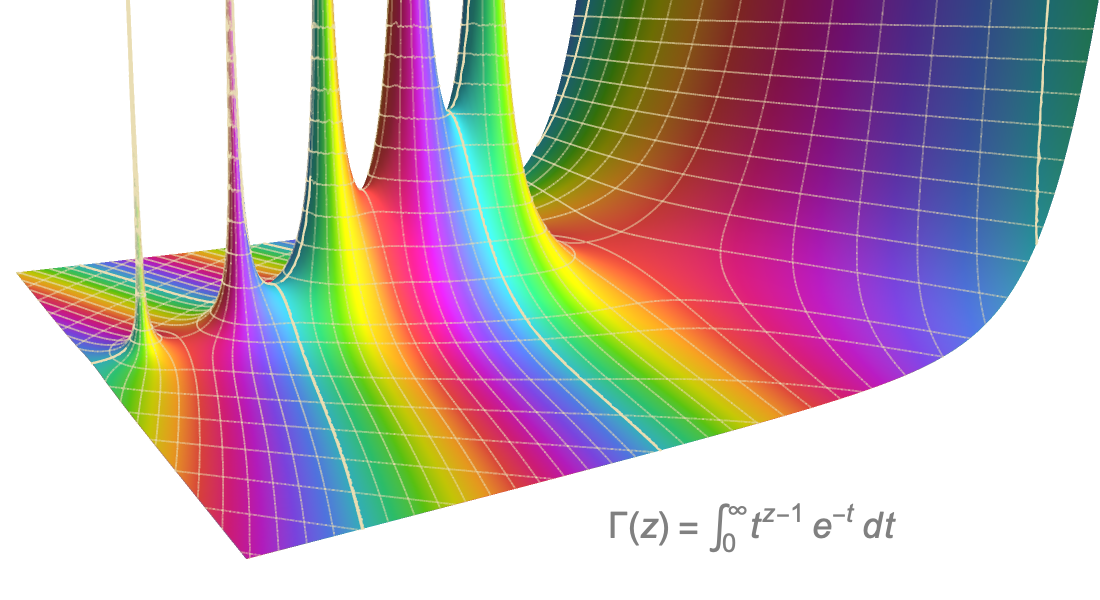
Mathematische Funktionen
Mit der Wolfram Language erhalten Nutzer Zugriff auf eine umfassende Sammlung spezieller Funktionen aus Physik, Technik, Statistik und anderen Bereichen. Neben elementaren Funktionen sind auch Bessel-, elliptische, hypergeometrische und weitere Funktionen integriert und können visualisiert, symbolisch vereinfacht oder mit beliebiger numerischer Genauigkeit ausgewertet werden.
Leitfaden zu mathematischen Funktionen »
Leitfaden zur Funktionsvisualisierung »
The Mathematical Functions Site »
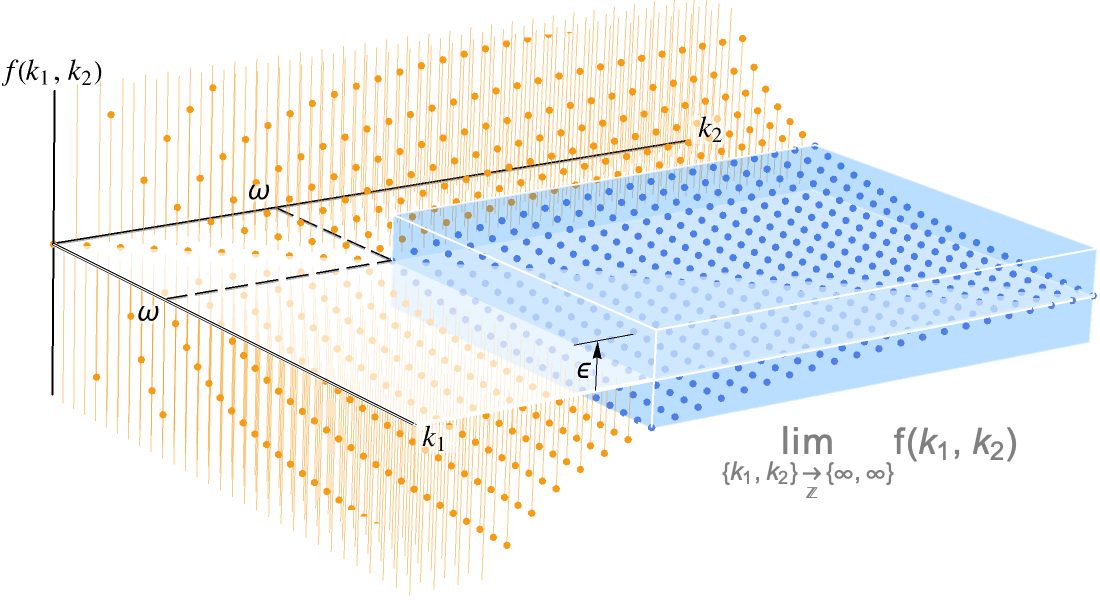
Diskrete Berechnungen
Nicht nur grundlegende Aufgabenstellungen in der Analyse von Algorithmen lassen sich mit der Wolfram Language lösen, sondern auch Aufgabenstellungen aus dem Bereich der numerischen Analyse und der Kombinatorik. Beispielsweise können mit der Wolfram Language endliche und unendliche Summen sowie Produkte berechnet oder Differenz- und Rekursionsgleichungen gelöst werden. Dazu haben Anwender Zugriff auf einen vollständigen Funktionssatz, der durch moderne Methoden unterstützt wird.
Asymptotische Berechnungen
Die Wolfram Language kann Näherungslösungen für schwierige Aufgabenstellungen mit Hilfe von asymptotischen Methoden als Ergänzung zu exakten symbolischen und numerischen Berechnungen finden. Der umfassende Katalog an automatischen Lösungsverfahren kann in einer Vielzahl von Bereichen eingesetzt werden, darunter z. B. Zahlentheorie, Analyse von Algorithmen, Wahrscheinlichkeitsrechnung und Statistik, theoretische Physik und numerische Analyse.
Integral- und Summationstransformationen
Mit der Wolfram Language lassen sich Daten oder Funktionen transformieren und so verschiedene Merkmale für Anwendungen in der Mathematik, Physik und Technik hervorheben. Symbolische und numerische Fourier-, Laplace-, Z- und weitere fortgeschrittene Tranformationen wie Hankel-, Radon- und Mellin-Transformationen helfen dabei, Differentialgleichungen zu lösen, Bilder zu analysieren und Merkmale in Signalen zu erkennen.
Leitfaden für Integral-Transformationen »
Leitfaden zu Summationstransformationen »
Leitfaden zur Fourier-Analyse »
Wolfram Solutions
Nächste Schulungen
| Mathematica - Grundlagen und Programmiertechniken 02.02. - 05.02.2026 - Online |
| Modul: Einführung in Mathematica 13.04.2026 - Online |
| Modul: CDF-Programmierung mit Mathematica 13.04.2026 - Online |
Nächste Webinare
| Wolfram-Webinar: Power up your Plots 29.01.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Schnelleinstieg in die Wolfram Language und den System Modeler 19.02.2026 : 11:00 - 11:45 Uhr |
| Wolfram-Webinar: Neuronale Netze mit Mathematica - Konstruktion & Anwendung 05.03.2026 : 11:00 - 11:45 Uhr |
Buchen Sie Ihren Termin mit unseren Spezialisten
| Name | Produkt | Themen | |
|---|---|---|---|
 |
Harald Farcas | Wolfram Mathematica, Wolfram Finance Platform, System Modeler, Wolfram Cloud Produkte und Origin/OriginPro | Industrie, Behörden, akademische Kunden, Product Manager Wolfram, Schulungen und Produktvorstellung |
 |
Ralf Rosenberger | Origin/OriginPro, Mathematica, Minitab | Produktapplikation, professioneller Service, Beratung, Rahmenvereinbarungen |
 |
Andreas Heilemann | Mathematica, Minitab, OriginPro | Enterprise Business, Großkunden, Senior Key-Account-Manager |