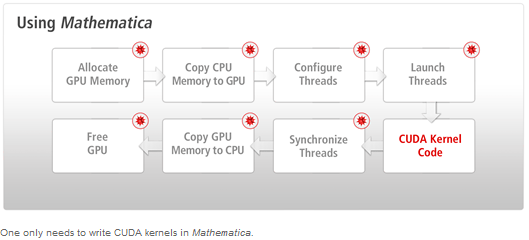
Mathematica and Cuda
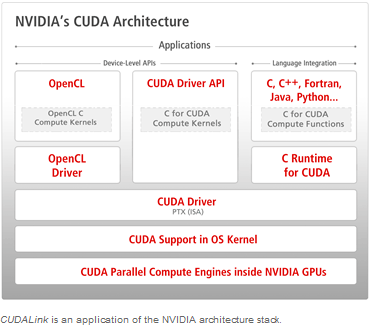
The Common Unified Device Architecture (CUDA) was developed by NVIDIA in late 2007 as a way to make the GPU more general. While programming the GPU has been around for many years, difficulty in programming it had made adoption limited. CUDALink aims at making GPU programming easy and accelerating the adoption. When using Mathematica, one need not worry about many of the steps. With Mathematica, one only needs to write CUDA kernels. This is done by utilizing all levels of the NVIDIA architecture stack.
CUDA Architecture
CUDA Architecture
CUDA's programming is based on the data parallel model. From a high-level standpoint, the problem is first partitioned onto hundreds or thousands of threads for computation. If the following is your computation,
OutputData = Table[fun[InputData[[i, j]]], {i, 10000}, {j, 10000}]|
, then in the CUDA programming paradigm, this computation is equivalent to: |
where fun is a computation function. The above launches 1000×1000 threads, passes their indices to each thread, applying the function to InputData, and places the results in OutputData. CUDALink's equivalence to CUDALaunch is CUDAFunction.
The reason CUDA can launch thousands of threads all lies in its hardware architecture. In the following sections we will discuss those, along with how threads are partitioned for execution.
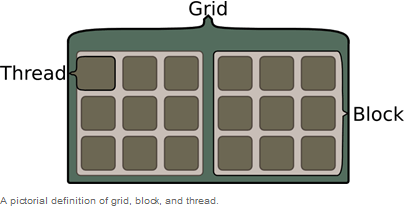
CUDA - Grid and Blocks
Unlike the message passing or thread-based parallel programming models, CUDA programming maps problems on a one-, two-, or three-dimensional grid. The following shows a typical two-dimensional CUDA thread configuration.
Each grid contains multiple blocks, and each block contains multiple threads. In terms of the above image, a grid, block, and thread are as follows.
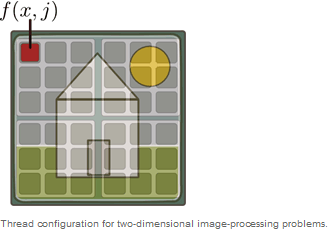
Choosing whether to have a one-, two-, or three-dimensional thread configuration is dependent on the problem. In the case of image processing, for example, we map the image onto the threads as shown in the following figure and apply a function to each pixel.
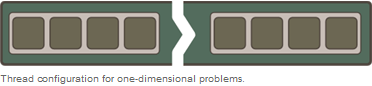
The one-dimensional cellular automation can map onto a one-dimensional grid.
CUDA Program Cycle
When programming in CUDA, the basic three steps are the following:
- Copy the data when launching threads.
- Wait until the GPU has finished the computation.
- Copy results from GPU back to host.
- Allocate memory of the GPU. GPU and CPU memory are physically separate, and the programmer must manage the allocation copies.
- Copy the memory from the CPU to the GPU.
- Configure the thread configuration: choose the correct block and grid dimension for the problem.
- Launch the threads configured.
- Synchronize the CUDA threads to ensure that the device has completed all its tasks before doing further operations on the GPU memory.
- Once the threads have completed, memory is copied back from the GPU to the CPU.
- The GPU memory is freed.
When using Mathematica, one need not worry about many of the steps. With Mathematica, one only needs to write CUDA kernels.
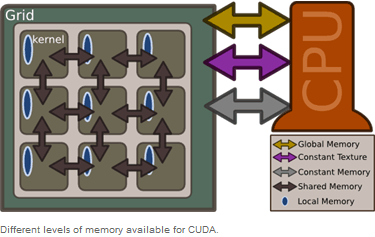
CUDA Memory Hierarchy
CUDA memory is separated into different areas; each of this memory areas has its advantages and restrictions. The image below shows all types of CUDA memory.
Global Memory
The main memory needs most of the space on a graphic board and is the slowest of the memories. All threads can use memory from the "global memory". Due to performance reasons, however, this should be avoided, if possible.
Texture Memory
The "texture memory" resides in the same area as the "global memory", but is read-only. By contrast it has a much higher performance. This memory only supports the values string, char, and int.
Constant Memory
This memory is a fast one, available for each thread from the grid. The memory is cached, but is limited to 64 kB globally.
Shared Memory
This memory as well is a fast memory, which is linked with one block respectively. Used with current hardware, this memory is limited to 16kB for each block.
Local Memory
This memory is local for each thread, but resides in the "global memory", until the compiler writes the variables into the registry. Here also, the access should be restricted to a minimum, even if this memory is not as slow as the "global memory".
CUDA Compute Capability
The "compute capability" specifies which operations are supported by the used hardware. Currently, the following operations are available:
| Compute Capability: |
Extra Features: |
| 1.0 | base implementation |
| 1.1 | atomic operations |
| 1.2 | shared atomic operations and warp vote functions |
| 1.3 | support for double-precision operations |
| 2.0 | double precision, L2 cache, and concurrent kernels |
If you have not imported CUDALink yet, please do it now:
Needs["CUDALink`"]
The following command shows all CUDA-enabled components of your system:
TabView[Table[
CUDAInformation[ii, "Name"] ->
CUDAInformation[ii,
"Compute Capabilities"], {ii, $CUDADeviceCount}]]
Multiple CUDA Devices
If system hardware allows, CUDA lets the user decide, which GPU is supposed to be used for computations. By default, the fastest GPU will be used, but the user can modify this setting. Once a GPU was selected, it cannot be changed during the kernel session.
Create a CUDA Kernel
The first Kernel
CUDA Kernel are atomic functions, performing the computation on each element of an input list. Our first kernel adds 2 elements.
__global__ void addTwo_kernel(int * arry, int len) {int index = threadIdx.x + blockIdx * blockDim.x;
if (index >= len) return;
arry[index] += 2;
}
__global __ is a function qualifier, which informs the compiler that this function shall be run on the GPU. __global__ functions can be called directly from C. The other function is __device__, defining functions that can be called by other functions like __global__ or __device__, but not from C.
A CUDA kernel must have a "void" output; to get a result, the input pointer must be overwritten. In this case, we pass an array and overwrite the elements (you may imagine that the array has the input/output parameters).
int index = threadIdx.x+blockIdx*blockDim.x;
Using the source code above, we get the index. The CUDA kernel provides us with the following variables, which will be set depending on the grid to be run and the block size.
- threadIdx - index of the current threads; the thread index is between 0 and blockDim -1
- blockIdx - index of the current blocks; the block index is between 0 and gridDim -1
- blockDim - the dimension of the block size
- gridDim - the dimension of the grid size
These parameters are set automatically by CUDA depending on the parameters that are passed when the kernel is started (block and grid dimension). Higher dimensions are set to 1 automatically, when launching a computation with lower dimensions. If you run a one-dimensional computation, .y and .z will be set to 1.
In most cases, you use threadIdx.x + blockIdx.x * blockDim.x in a 1D grid to find the global offset. To determine the global position in 2, threadIdx.x + blockIdx.x * blockDim.x + (threadIdx.y + blockIdx.y * blockDim.y)*width is used.
if (index >= len) return;
Since threads are run on multiples of the block dimension, the user must ensure not to overwrite the limits, provided that the input dimension is not the multiple of the block dimension. This can be assured by:
in[index] += 2;
This function is applied to each element of the list; here, 2 is added to each element.
The second Kernel
The second kernel implemented a finite method of differentiation:
__device__ float f(float x) {
return tanf(x);
}
__global__ void secondKernel(float * diff, float h, int listSize) {
int index = threadIdx.x + blockIdx.x * blockDim.x;
float f_n = f(((float) index) / h);
float f_n1 = f((index + 1.0) / h);
if( index < listSize) {
diff[index] = (f_n1 - f_n) / h;
}
}
This is a device function. __device__ functions can be called by the __global__ function, but cannot be run directly from Mathematica.
return tanf(x);Perform tangent on a float input.
__global__ void secondKernel(float*diff, float h, int listSize) {Function, which outputs the list diff and takes the scalar sizes h and listSize.
int index=threadIdx.x+blockIdx.x*blockDim.x;Delivers the global thread offset.
float f_n=f(((float) index)/h);Evaluates the function at index/h. Index and h are type int, thus, we must convert the result according to float in order to avoid an abort.
float f_n1=f((index+1.0)/h);Evaluates the function at (index+1)/h.
if(index<listSize) {Avoids that the output buffer gets overwritten.
diff[index]=(f_n1-f_n)/h;Computes the difference and saves the result in diff.
Load CUDA Kernel in Mathematica
Load CUDA Kernel in Mathematica
If you have not loaded the CUDALink yet, please do it now.
Needs["CUDALink`"]We save the created program in a string.
secondKernelCode = "__device__ float f(float x) {
return tanf(x);
}
__global__ void secondKernel(float * diff, float h, int listSize) {
int index = threadIdx.x + blockIdx.x * blockDim.x;
float f_n = f(((float) index) / h);
float f_n1 = f((index + 1.0) / h);
if( index < listSize) {
diff[index] = (f_n1 - f_n) / h;
}
}";
The CUDA function is loaded. We pass the kernel code as first argument, the running kernel name ("secondKernel") as second argument, the function parameter as third argument, and the block size as fourth argument. The result will be saved in secondKernel.
secondKernel =
CUDAFunctionLoad[secondKernelCode,
"secondKernel", {{"Float"}, "Float", _Integer}, 16]
In the background, the following happens:
- CUDA availability is checked.
- CUDA code is compiled into a binary and optimized for the respective GPU.
- CUDA code is cached to avoid later compilation.
- It is checked, if the kernel from the CUDA code exists.
Once loaded, the CUDA function can be used like a Mathematica function. Before we can start, we need a memory to save the result in.
buffer = CUDAMemoryAllocate["Float", 1024]
Here, we run the second CUDA kernel.
secondKernel[buffer, 100.0, 1024]
The following command provides the first 30 elements from the output buffer.
CUDAMemoryGet[buffer][[;; 30]]

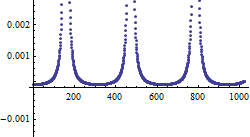
Our result is plotted accordingly:
ListPlot@CUDAMemoryGet[buffer]
The buffer must be cleared again by the user.
CUDAMemoryUnload[buffer];