Mathematica Ausführlich
Mathematica ist das integrierte System für die vollständige Entwicklung, Berechnung, Simulation, Analyse und Dokumentation von technischen Problemstellungen in einer einheitlichen, plattformunabhängigen Arbeitsumgebung unter Einsatz der Wolfram Language. Mit der revolutionären "One-Klick"-Runtimeerstellung zur Weitergabe der Ergebnisse mit der Mathematica-Player-Technologie - und damit einem beispiellos einfachen Workflow - ist Mathematica die ideale, technische Entwicklungsumgebung mit automatisierter Runtime-Erstellung geworden. Mathematica integriert dazu noch parallelisierte Technologien, um Ihre Multicore-PCs voll auszulasten und erlaubt es, selbst C-Code zu generieren.
Mathematica eröffnet dem Nutzer eine nahezu unendliche Vielfalt an mathematischen Funktionen zur Lösung von Aufgaben aus dem Ingenieurwesen, der Finanz- und Versicherungsmathematik, der Mathematik, der Statistik, der Physik, dem "Chemical Computing" und allen anderen Naturwissenschaften.
Dem Anwender gegenüber präsentiert sich Mathematica mit seiner revolutionären - da plattformübergreifend identischen - Benutzeroberfläche, dem Notebookinterface.
Wolfram Research hat für den Anwender zwei bahnbrechende Technologien integriert, beide unter Integration von Wolfram|Alpha, mit denen das Arbeiten in Mathematica besonders einfach ist.
- Compute-As-You-Think-Technologie: Eingaben können in nativer englischer Sprache gemacht werden.
- Wolfram-Predictive-Interface: Diese Technologie bietet Ihnen eine vorausschauende Funktionsauswahl sowie Funktionsvorschläge für Ihre potenziell nächsten Schritte. Dieses neue Konzept beruht auf der Analyse von Millionen von Nutzeranfragen an die wissenschaftliche Suchmaschine Wolfram|Alpha.
- Wolfram-Cloud-Anbindung: Mathematica (Desktop Variante) kann sich integrativ mit einer/oder mehreren der bestehenden Wolfram-Cloud-Lösungen verbinden (kann bei Bedarf, also NICHT automatisiert). Dadurch lassen sich Ergebnisse, Simulation, dynamische Objekte, wiederum per "One-Klick" im Internet mit einer eigenen URL sofort veröffentlichen, und das ohne jegliche Websatzkenntnisse, alles in der Wolfram-Cloud.
Übersicht
Was ist Mathematica
Mathematica ermöglicht die vollständige Entwicklung, Berechnung, Simulation, Analyse und Darstellung von technischen Problemstellungen in einer einheitlichen, plattformunabhängigen Arbeitsumgebung und wird deshalb auch als ein System für Technical Computing und Technical Publishing bezeichnet. Es ist eines der weltweit am meisten verbreiteten Softwaresysteme für technische Berechnungen. Mit Mathematica erhält der Benutzer ein mächtiges Werkzeug an die Hand, mit dem sich sowohl kleine als auch sehr komplexe Aufgaben aus der Mathematik, Physik, den Ingenieur- und Finanzwissenschaften u.a. lösen lassen.
Neben den mathematischen Fähigkeiten hat sich Mathematica auch als Programm mit weitreichenden Grafikmöglichkeiten einen Namen gemacht und bietet zudem die Anwendung der analytischen Fähigkeiten auch zur Grafikbearbeitung an. Diese beschränken sich nicht nur auf qualitativ hochwertige 2D- und 3D-Grafiken sowie Echtzeitgrafiken, sondern erlauben auch die Erzeugung von Animationssequenzen ("Filmen") als Movies oder Flash-Animationen. Mathematica ist damit auch eines der wenigen Softwaresysteme, in welchem sich technische Zusammenhänge direkt in Flash© wandeln lassen.
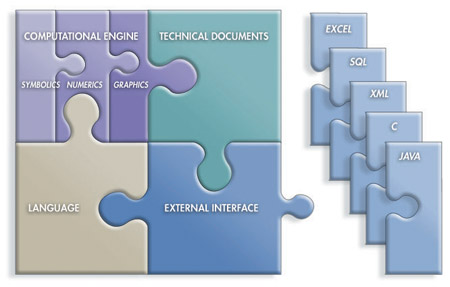
Das Mathematica-System besteht aus zwei Teilen, dem sog. Front-End (graphische Benutzeroberfläche) und den Kernels (Kernen). Das Front-End schickt Anfragen an den Mathematica Kern, der die eigentlichen Berechnungen ausführt, d.h. die Anfragen beantwortet und diese zur Darstellung an die Benutzeroberfläche zurückgibt.
Kernbereiche
Um die Mächtigkeit von Mathematica einordnen zu können, ist es wichtig die Kernbereiche/Kerntechnologien zu verstehen.
Einfacher geht es nicht
Mit Mathematica erhalten Sie ein Werkzeug, mit welchem Sie sofort nach der Installation loslegen können, denn alle Funktionen folgen der gleichen Syntax und sind ausführlich im Hilfesystem (über 1600 Buchseiten zu Anwendung und Mathematik) erklärt. Das Hilfesystem ist zudem nicht statisch, sondern erlaubt das direkte Berechnen und Testen der Funktionen im Hilfesystem.
Mit Mathematica erledigen Sie einzelne Aufgaben - beispielsweise das Auswerten von Messdaten oder die Lösung einer schwierigen Differentialgleichung - genauso, wie Sie komplette Lösungen von der ersten Idee bis zum fertigen Softwaresystem entwickeln.
Einzigartige Rechenpower und einfache Bedienung
Profitieren Sie von der einzigartigen Kombination einer intuitiven Bedienoberfläche mit den legendären Rechenfähigkeiten in Mathematica, verbunden mit Multicore-Technologie und Multithreading. Mathematica unterstützt Parallelcomputing dadurch, dass der Anwender mehrere Rechenkerne parallel arbeiten lassen kann und zwar ohne jegliche Kenntnisse vom Parallelisieren von Berechnungen. Die Parallelverarbeitung ist vollautomatisch integriert in Mathematica ab V8.
- Vordefinierte Paletten zur Eingabe und Befehlsauswahl
- Programmierbare Benutzeroberfläche
- Interaktives und erweiterbares Hilfesystem
- Editier- und ausführbare Beispiele
Sie klicken mit Hilfe der eingebauten Paletten mathematische Ausdrücke einfach zusammen oder rufen damit Funktionen und Befehle auf. Mit der voll programmierbaren Benutzeroberfläche ermöglichen Sie den Zugriff auf Funktionen oder eigene Pakete beispielsweise durch selbstdefinierte Paletten und Schaltflächen.
Kommunikativ
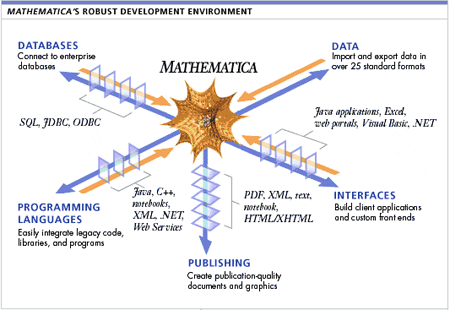
Mathematica ist kein proprietäres, sondern ein nach allen Seiten offenes und standardisiertes System, das sich nahezu beliebig anpassen lädt. Es besteht aus mehreren plattformunabhängigen Komponenten, die für den Nutzer meistens unsichtbar im Hintergrund die Arbeit verrichten:
- Der mathematische Kernel (sozusagen das Wissensbuch der Mathematik).
- Das plattformunabhängigen Notebookinterface (das Front-End: identisch für Windows, Macintosh, Linux, Unix bis V7).
- MathLink, das Kommunikationsprotokoll zwischen Kernel und der Benutzeroberfläche und anderen Systemen
- MathML zur Darstellung von Formeln im WWW.
- J/Link, die Schnittstelle zu Java.
- .NET, die Schnittstelle zu Microsoft
- Datenbanken und Webservices
- MathLM, die Lizenzmanagersoftware zur Kontrolle und Steuerung der Zugriffe.
Aufgrund der offenen Standards ist es möglich, den mathematischen Kernel an nahezu jede andere Software oder Benutzeroberfläche anzudocken. So sind z. B. Zusatzmodule zur direkten Anbindung an Microsoft Excel, Microsoft Access, Origin, LabView, Oracle u. a. verfügbar. Selbst dem Internet gegenüber zeigt sich der Kernel via J/Link offen und kann als webMathematica die unternehmensweite Berechnungsengine sein oder kann einfach als Black-Box im Hintergrund von web-basierten Analysen und Graphen seine Arbeit verrichten.
Lassen Sie sich durch die vielen integrierten Standards nicht verwirren! Das ist die globale Erfolgsstrategie von Mathematica - nicht geschlossen sondern offen für die Welt.
Programmiersprache
Eingebaute Programmiersprache
Die eingebaute Programmiersprache ist einer der entscheidenden Faktoren für den weltweiten Erfolg von Mathematica und den Ruf, das Tool für den Entwicklungsingenieur am Computer zu sein. Die Architektur ist klar definiert und exakt durchkonstruiert. Funktionsargumente sind eindeutig definiert und komplizierte Programmstrategien sind nicht notwendig.
Das System erlaubt verschiedene Programmierstile, darunter prozedural, funktional (APL, C,PASCAL), regelbasiert (Prolog), objektorientiert (C++) und die Mustererkennung (Pattern Matching). Symbolische Programmierung, funktionale Programmierung und Pattern Matching sind zentrale Mechanismen in Mathematica.
Seit Mathematica 8 lässt sich in Mathematica ein eigener C-Compiler integrieren; mehr zur C-Compiler-Integration.
Regelbasierter Ansatz
Der regelbasierte Ansatz ermöglicht es, Umwandlungsregeln für mathematische Ausdrücke zu spezifizieren. Jede Regel hat Bezug auf ein Modell und agiert als ein Ausdruck, der das Modell abbildet. Eine Vielzahl der Regeln kann durch direkte Umsetzung von Formeln aus Büchern konstruiert werden. Regeln können einen Namen erhalten und bei Bedarf aktiviert werden oder in einer globalen Regelbasis so implementiert sein, dass diese immer verfügbar sind. Die Programmiersprache Mathematicas ist eine Hochsprache, die den Anwender in die Lage versetzt, komplexe Programme zu erstellen, die aus einfachen, nicht-kryptischen Funktionsaufrufen bestehen, welche direkt auf die nativen Operationen in Mathematica selbst zugreifen. Viele solcher Programme sind in Form von Mathematica-Paketen verfügbar. Diese Pakete wurden von Mathematica-Nutzern über die Jahre hinweg erstellt und sind an die verschiedensten Anwendungen angepasst. Mit über 3000 eingebauten Funktionen stellt Mathematica eine extrem mächtige Programmiersprache dar, welche durch eigene Funktionen erweitert werden kann.
Alles ist ein Ausdruck
In Mathematica ist alles ein Ausdruck, so auch das Notebook und die Formatierungen der Texte. Dies ermöglicht das vollautomatische Erzeugen von Reports und Paletten und die Bearbeitung von Dokumenten. Jedes Detail eines Mathematica Dokumentes kann damit von einem Programm aus einfach formatiert werden.
Mathematik und Algorithmen
Vielfalt
Mathematica bietet eine große Anzahl interner Funktionen an. Damit könnte man Mathematica auch als eines der größten Formelwerke der Mathematik bezeichnen, sozusagen wie ein elektronischer Bronstein. Nachfolgend eine unsortierte Auswahl von Mathematica-internen Funktionen:
- Verteilungsfunktionen (Beta, Cauchy, Chi-Square, exponentiell, Extremwert/Fisher-Tippett, F-Ratio, Gamma, Normalverteilung, Laplace, Rayleigh, Weibull, Wahrscheinlichkeitsdichte, kumulative Verteilung, Quantile, Mittelwert, Varianz, Standardabweichung, Verschraubung, Kurtosis, Bernoulli, binomial, diskret-uniforme Verteilung, geometrische, hypergeometrische, Poisson u. w.).
- Elementare transzendente Funktionen (exponential, logarithmisch, trigonometrisch u. inverse, hyperbolische u. inverse).
- Zahlentheorie (ggT, kgV, Primzahlen, Primfaktoren, Funktionen von Moebius u. Euler, Jacobi Symbol u. w.)
- Elliptische Integrale und Funktionen.
- Kombinatorik (Binomial- u. Multinomialkoeffizienten, Bernoulli- u. Euler-Zahl/-Polynom, Stirling Zahlen, Permutation, Clebsch-Gordan Koeffizient u. w.).
- Orthogonale Polynome (Legendre, sphärisch-harmonische, Gegenbauer, Chebyshev, hermitäische, Laguerre, Jacobi).
- Spezielle Funktionen (Airy, Bessel, Euler-Beta, Sinus/Cosinus-Integral, Fehler-Funktion, Exponential-Integral, Gamma, hypergeometrische, Legendre, Lerch's transzendente, Pochhammer, Poly-Gamma, Riemann-Siegel-Theta, Riemann-Zeta).
Numerische Berechnung
Mathematica enthält eine Vielzahl hochentwickelter Algorithmen zur numerischen Lösung, z. B. in der Matrizenrechnung und Integration, beim Lösen von Differentialgleichungen, bei der Optimierung und dem Auflösen von Gleichungen. Mathematica wählt dabei den am besten geeigneten Algorithmus zu dem mathematischen Problem aus. Der Anwender formuliert lediglich die mathematische Aufgabe.
Bei Mathematica gibt es so genannte Überfunktionen, wie z.B. Solve[]. Der Anwender gibt lediglich den Befehl ein und überlässt es Mathematica, den geeigneten Solver zu finden; ganz im Gegensatz zu anderen Systemen, bei denen sich der Anwender mit einer Vielzahl an Kommandos zum Lösen von Gleichungen auseinandersetzen muss.
Es ist auch möglich, dass der Anwender den Algorithmus manuell festlegt, oder bei einigen numerischen Funktionen wie NDSolve[] seinen eigenen Solver implementiert. Spezielle Optionen erlauben dem Anwender das Überwachen und Verfeinern des Lösungsprozesses.
Mathematica arbeitet mit Zahlen beliebiger Größe und Genauigkeit. Hierdurch erhält der Anwender die vollständige Kontrolle über numerische Rundungsfehler. Dies erlaubt eine Vielzahl von Berechnungen mit sowohl theoretischem als auch praktischem Anspruch, die mit normalen wissenschaftlichen Taschenrechnern oder Programmiersprachen nicht möglich wären. Mathematicas wahlfreie numerische Genauigkeit ermöglicht ein breites Anwendungsfeld an mathematischen Funktionen: Exponentialfunktionen, Bessel-Funktionen, hypergeometrische Funktionen, elliptische Integrale u.v.m.
Mathematica kann alle symbolischen Operationen und Funktionen auch numerisch berechnen: Polynom-Interpolation und -Extrapolation, Fouriertransformation, Nullstellenbestimmung, lineare und nichtlineare Optimierung sowie Kurvenanpassung mit komplett frei definierbaren Funktionen (linear und auch nicht-linear, quadratisch, Polynom, logarithmisch,...).
Erfahren Sie mehr zu den Funktionen der numerischen Berechnung und speziell zu Wolfram gigaNumerics.
Symbolische Berechnung
Neben den herausragenden numerischen Rechenmöglichkeiten steht dem Anwender von Mathematica symbolische Mathematik zur Verfügung. In Mathematica implementiert sind die Standardoperationssymbole der Algebra und Analysis einschließlich die der Integration, Differentiation und Polynomberechnung.
Der Anwender von Mathematica kann sich explizit Formeln als Gleichungslösung anzeigen lassen; dies ist manchmal für das Verständnis der kompletten Struktur einer Lösung einfacher als numerische Resultate. Mathematica erkennt selbständig mögliche Fallunterscheidungen, die zu einer vollständigen Beschreibung der Ergebnisse notwendig sind.
Mathematica enthält eine große Sammlung von symbolischen Transformationsregeln, die das Manipulieren und Vereinfachen komplexer Formeln erlaubt. Die Manipulation und Ableitung exakter algebraischer Formeln befähigt den Anwender dazu, eine breite Palette von Berechnungen zu automatisieren, welche bisher nur per Hand erledigt werden konnten.
- Eine detaillierte Liste der symbolischen Funktionen - wobei auch diese nicht vollständig ist - finden Sie auf der Feature-Liste.
Symbolik für Ingenieure
Als Alternative zu herkömmlichen, rein numerischen Methoden, wie Finiten Elementen, gewinnt die Computer-Algebra gestützte Simulation in zahlreichen Gebieten an Bedeutung. Mathematica beherrscht beide Methoden und erlaubt den direkten Vergleich der Ansätze in einem System! Aus diesem Grund hat sich Mathematica in den letzten zwei Jahren, aus dem universitären und wissenschaftlichen Bereich kommend, mehr und mehr in der Forschung und Entwicklung im industriellen Einsatz bewährt. Projekte, wie die Entwicklung einer Radbahn für die olympischen Spiele in Atlanta, der Einsatz in der MIR-Raumstation oder im Risikomanagement der Finanzwelt, zeigen diesen Trend.
Die integrierte hochentwickelte Programmiersprache ermöglicht Rapid Prototyping, d. h. die direkte Umsetzung von Ideen und Algorithmen in "computerverständliche" Form.
Datenverarbeitung & Datenquellen
Integrierte Funktionen
Die integrierten Funktionen von Mathematica stellen jedoch nur einen kleinen Teil des gesamten Funktionsumfangs dar. Nahezu noch bedeutender für ein System für Technical Computing und Technical Publishing ist die Offenheit, um Daten aus jeglichen Datenquellen einzulesen und zu verarbeiten.
Kurz aufgelistet bestehen die Unterbereiche bei der Datenverarbeitung aus:
- Import und Export
- Arrays
- Numerischen Daten
- Bildverarbeitung
- Signalverarbeitung
- Text-Verarbeitung (String-Manipulation)
- Binärdaten
- Dateien
- Datenbanken
- Zeit und Datum
- Integrierte Datenquellen
Einige dieser Themen werden im Folgenden weiter erklärt.
Datenimport und Export
Mathematica verarbeitet automatisch Hunderte von verschiedenen Datenformaten und Unterformaten - alle konsistent eingebunden über die symbolischen Fähigkeiten von Mathematica. Mathematica bietet verschiedene Möglichkeiten, um den Datenaustausch zu externen Programmen zu gestalten. Am einfachsten funktioniert dies über Dateien im ASCII- oder Binärformat. Mathematica liest z. B. numerische Daten wie sie Tabellenkalkulations- und Datenbankprogramme produzieren. Grafiken können in den Grafikformaten von Desktop-Publishing-Systemen wie Adobe Illustrator, Adobe Indesign, Animationspaketen oder im AVI-Format exportiert werden. Spezielle "Print Forms" lassen sich definieren, um symbolische oder numerische Ergebnisse zu exportieren, die in C oder FORTRAN implementiert werden können. Auch die Ausgabe und der Import in der Schriftsetzersprache TeX ist möglich.
Mathematica kann auch an andere Anwendungsprogramme mittels MathLink bzw. J/Link direkt angekoppelt werden (siehe MathLink), so wird zum Beispiel die Anbindung an eigene C++ - oder Java-Programme möglich. Der .NET/Link™ ermöglichen den Entwicklern, Mathematica in Anwendungen zu integrieren, die Microsofts .NET Technologie einsetzen wollen.
Datenbanken, "Data Sources" - Datenquellen
Mathematica stellt nicht nur Funktionen zur Verfügung sondern auch "Data Sources". Einige sind den Anwendern seit Jahren bekannt wie PolyhedronData, GraphData, KnotData, LatticeData. Ab Mathematica V8 sind hinzugekommen z. B. ChemicalData, IsotopData, ParticalData, AstronomicalData, CountryData, CityData, FinancialData,..
Einige dieser Datenquellen sind mit den Servern von Wolfram Research verknüpft und lassen sich vom Anwender gesteuert auf der eigenen Festplatte aktualisieren. Wolfram stellt dieses als neuen und wichtigen Dienst zur Verfügung.
Über den integrierten DataBaseLink können zusätzlich alle gängige Datenbanken, z.B. Oracle, MS Access, mySQL, in Mathematica integriert werden. Des Weiteren werden WebServices durch WSDAL (web services description language) vollständig in Mathematica unterstützt.
Der MathLink Kommunikationsstandard (für Programmierer)
MathLink ist das Mathematica Kommunikationsprotokoll. Auf diesem Weg werden Daten und Kommandos zwischen Mathematica und anderen Programmen ausgetauscht. Die aktuelle MathLink-Bibliothek ist für C Programme geschrieben, geplant ist die Unterstützung weiterer Programmiersprachen. MathLink bietet folgende Einsatzmöglichkeiten:
- Betrieb des Mathematica-Kernels auf Remote-Server über RSH oder SSH möglich.
- Aufruf externen Codes von Mathematica aus. Rechenintensive Funktionen können so beispielsweise durch Verwendung spezieller Numerik-Bibliotheken (NAG, ISML, ...) beschleunigt werden.
- Aufruf Mathematicas als Unterprogramm von einem anderen Programm aus. Der gesamte Funktionsumfang Mathematicas, einschließlich aller Grafik-Funktionen, steht so dem externen Programm zur Verfügung. Beispielsweise kann Mathematica an Datenbanken oder Kalkulationsprogramme angebunden werden.
- Mathematica kann von Mathematica aufgerufen werden. Dies ist eine ideale Experimentierumgebung zum Parallelisieren von Algorithmen. Komplexe Aufgaben können auf kleine Teilaufgaben reduziert werden.
- Lesen Sie hier weitere Informationen zum MathLink-Standard
Die MathLink-Bibliothek enthält alle Funktionen, die notwendig sind, um mit MathLink zu arbeiten. Dazu gehören Funktionen zum Öffnen und Schließen des Links sowie zum Senden und Empfangen von Mathematica-Ausdrücken. Die MathLink-Funktionen sind plattformunabhängig, d.h. MathLink-Programme können auf jeder Plattform kompiliert werden. Eine aufwändige Portierung entfällt. In Wolfram Researchs Documentation Center sind darüber hinaus zahlreiche Beispiele vorhanden.
Dynamische Interaktivität
Dynamische Interaktivität
Mit Mathematica 6 integrierte Wolfram Research nicht nur über 1000 neue Funktionen, sondern entwickelte eine vollkommen neue Technologie - die Dynamische Interaktivität.
Mit dem einfach Befehl "Manipulate" und der Angabe, welche Parameter dynamisch betrachtet werden sollen, lässt sich aus einem Mathematica-Befehl ein dynamisches Objekt mit eigener GUI erstellen. Die GUI (Benutzeroberfläche) wird vollautomatisch erstellt und enthält mit den Parametern verknüpfte Slider, Buttons, Pop-Ups, etc. Alle Elemente passen sich nahtlos in das Design ein. Einfacher kann es nicht gehen!
 Mathematica's Manipulate Command
Mathematica's Manipulate Command
(1:18)
Tauchen Sie ein in die interaktive Welt der Visualisierung. Das "Wolfram Demonstration Projekt" zeigt viele Tausend solcher interaktiven Beispiele.
Visualisierung und Grafik
Visualisierung und Grafik
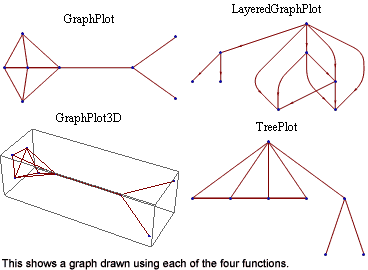
Mathematica ermöglicht es, Funktionen und Daten zweidimensional und dreidimensional, in Farbe oder schwarzweiß und in Form vieler Einzelgraphen auch als Film darzustellen. Die Graphen werden automatisch skaliert, lassen sich aber auch den Benutzeranforderungen entsprechend gestalten. Die Graphen können hinsichtlich Kurven- und Strichtyp, Farbe, Stil und Achsen angepasst werden. Legenden, Beschriftung, Umrahmung, Hintergründe sind ebenfalls einstellbar. Nachfolgend einige Typen: Funktions-Diagramme, parametrisierte Darstellung, Konturplots, Dichteverteilungen, Arrayplots, Netzwerkgraphen, Oberflächendarstellung (Drahtmodell oder Schattierung mit Beleuchtung,...), 3D-Graphiken (mit Entfernung verdeckter Kanten und Flächen,...), spezielle statistische Graphiktypen (Balken- und Kuchendiagramme, Paretoplot, logarithmische Diagramme, Polarplot, sphärische 3D-Plots,...).
Mathematica erzeugt dreidimensionale Farbbilder symbolischer Beschreibungen arbiträrer geometrischer Objekte. Zum Beispiel können Mathematicas Fähigkeiten zur symbolischen und zur numerischen Berechnung verwendet werden, um eine Liste von Ansichten eines komplexen Polyhedrons zu erzeugen. Hieraus lässt sich über Mathematicas Grafikfähigkeiten ein dreidimensionales Bild erstellen. Der Anwender erhält eine dynamische Simulation oder die Veränderungen der Grafik bei Variation einer oder mehrerer Parameter. Mathematica verwendet für jede grafische Ausgabe POSTSCRIPT. Diese größen- und auflösungsunabhängige Seitenbeschreibungssprache produziert auf Medien wie Computerbildschirmen, Laserdruckern, Photosatzmaschinen und anderen Ausgabegeräten Reports in Präsentationsqualität, Farbnegative für Zeitschriften und Bücher oder sogar riesige Poster. Mathematica erlaubt es, Grafiken in vielen Grafikformaten zu speichern, auch im Encapsulated-POSTSCRIPT-Format. Damit können die Grafiken leicht in Dokumente anderer Programme eingefügt werden, z. B. in Desktop-Publishing-Programmen.
Notebook-Konzept und Dokumentation
Notebook-Konzept
Das System Mathematica besteht aus zwei Teilen, dem sog. Front-End=Notebook (graphische Benutzeroberfläche) und den Kernels (Kern). Das Front-End schickt Anfragen an den Mathematica Kern, der die eigentlichen Berechnungen ausführt, d.h. die Anfragen beantwortet und diese zur Darstellung an die Benutzeroberfläche zurückgibt.
Die vom Mathematica-Front-End erzeugten interaktiven elektronischen Dokumente heißen Notebooks. Die Notebook-Schnittstelle ist Teil der graphischen Benutzeroberfläche von Mathematica.
Mathematica Notebooks sind vollständig interaktive Dokumente, die Text, Tabellen, Formelsatz, Graphik, Töne, Berechnungen, Simulationen und Animationen in einem Benutzerinterface kombinieren.
Die meisten Textverarbeitungs-Eigenschaften des Front-Ends wie Schriftart, Schriftstil, Größe, Farbe, Hintergrund-Farbe etc. sind unter dem Format Menü zu finden. Formeln wie ![]() lassen sich problemlos als so genannter InlineInput in Textzeilen einbetten. Neben den Zeichen auf der Tastatur gibt es noch Hunderte von Sonderzeichen und Symbolen wie z.B. Ø . Bequem für die Eingabe von Sonderzeichen sind Paletten wie CompleteCharacters oder
lassen sich problemlos als so genannter InlineInput in Textzeilen einbetten. Neben den Zeichen auf der Tastatur gibt es noch Hunderte von Sonderzeichen und Symbolen wie z.B. Ø . Bequem für die Eingabe von Sonderzeichen sind Paletten wie CompleteCharacters oder
InternationalCharacters.nb
Symbolpaletten
Die Eingabe von Formeln, Vektoren und Matrizen erfolgt über die Tastatur oder über Symbolpaletten. Per Mausklick lassen sich komplexe Aufgaben schnell eingeben. Das Umsetzen von mathematischen Formeln in die Mathematica-Sprache führt Mathematica durch, der Anwender gibt seine Berechnungen so ein, wie er sie auf dem Papier notiert bzw. wie sie in der mathematischen Literatur dargestellt werden.
Über die vordefinierten Symbolpaletten hinaus können oft benötigte Funktionen in selbstdefinierten Paletten zusammengestellt werden. Diese Paletten können separat verwaltet oder aber in Notebooks integriert werden. Der Anwender ist so vollkommen losgelöst von der Mathematica-Syntax. Der Hilfe-Browser enthält nicht nur Referenzen zu den eingebauten Funktionen, sondern das komplette "Mathematica Buch" (Englisch) einschließlich aller Beispiele. Die Beispiele können im Hilfe-Browser modifiziert und direkt berechnet werden. Die elektronische Hilfe stellt damit eindrucksvoll die elektronischen Publikationsmöglichkeiten von Mathematica dar.
Einige Symbolpaletten finden Sie unter Symbole und Formeleditor
Mathematische Ausdrücke können auf drei verschiedene Arten dargestellt werden:
- In der Mathematica Syntax.
- In einer Kombination aus Mathematica Syntax und Formeldarstellung, wobei die wichtigsten Symbole (Integrale, Summen, Produkte, Unendlich, ...) in mathematischer Formelschreibweise dargestellt werden.
- In traditioneller mathematischer Form (so wie es im Lehrbuch steht!); die Ausgabe entspricht hierbei der Formeldarstellung in TeX.
Die Ausdrücke können jederzeit von einem in das andere Format konvertiert werden. Es ist möglich, Teile eines mathematischen Ausdruckes einzeln zu berechnen und das Ergebnis in den Ausdruck einzufügen, ohne separate Ein- und Ausgabezeile.
Schriftsatz
Mathematica eignet sich aufgrund der eingebauten Schriftsatzfähigkeiten ganz hervorragend zur Dokumentation. Seine Architektur erlaubt die Nutzung von portablen Stylesheets (Dokumentvorlagen). Durch die Kombination von Texten, Grafiken, Tönen, Animationen, Hypertext und Links zu externen Dateien wird Mathematica zu einem einmaligen Publikationssystem zur Repräsentation von Wissen. Fähigkeiten zur automatischen Nummerierung von Gleichungen, Kapiteln und Abschnitten sowie die Möglichkeit, beliebige Zeichensätze einzubinden, erweitern Mathematica zu einem vollwertigen mathematischen Publikationswerkzeug. Via Hyperlinks werden Querverbindungen in Mathematica-Dokumente eingefügt, per Mausklick springt der Anwender zu den entsprechenden Stellen. Mathematica erlaubt das Speichern der Dokumente in TeX oder auch HTML.
Die meisten Textverarbeitungs-Eigenschaften des Front-Ends wie Schriftart, Schriftstil, Größe, Farbe, Hintergrund-Farbe etc. sind unter dem Format Menü zu finden. Formeln wie ![]() lassen sich problemlos als sog. InlineInput in Textzeilen einbetten.
lassen sich problemlos als sog. InlineInput in Textzeilen einbetten.
Hilfesystem
Mathematica wird ohne gedruckte Dokumentation geliefert - das benötigt es auch gar nicht. Beim Hilfesystem von Mathematica zeigt Wolfram Research eindrucksvoll einen Teil seiner Technologie. Das interaktive vollständige Hilfesystem ist mit den Webressourcen bei Wolfram Research verknüpft und integriert die Online-Resourcen damit in das Hilfesystem. Das frühere Mathematica Buch ist vollständig im Hilfesystem enthalten.
Die Beispielfunktionen im Hilfesystem lassen sich verändern und neu berechnen.
Wolfram|Alpha Integration
Compute-As-You-Think-Technologie
Seit Mathematica 8 ist eine Schnittstelle zu Wolfram|Alpha integriert, über welche die Freiformeingabe "Compute-As-You-Think" in nativer englischer Sprache in Mathematica möglich ist, mit deren Hilfe Sie direkt aus Mathematica heraus Wolfram|Alpha befragen können und die Antwort in Ihrem Notebook platziert bekommen.
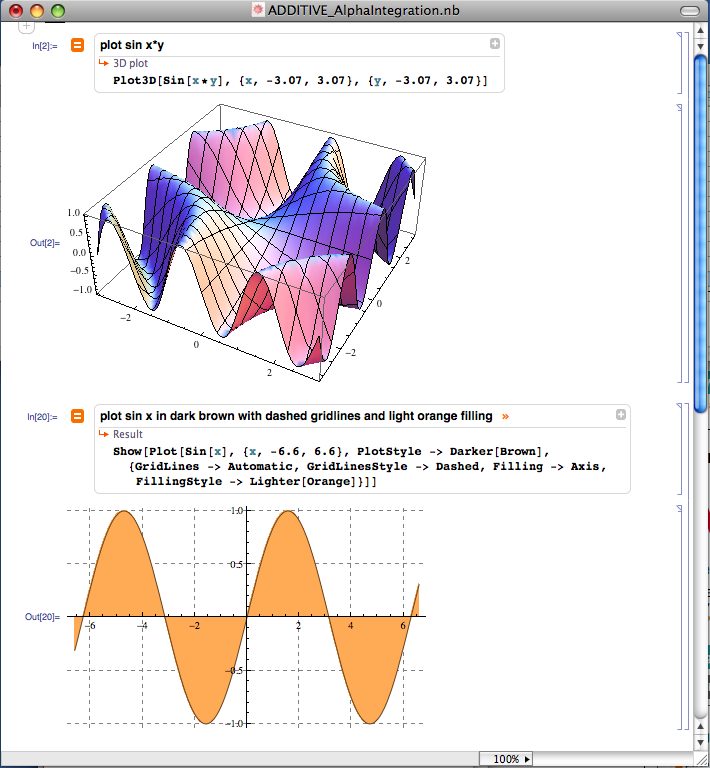
Mathematica Freiform Eingabe (Anklicken zum Vergrößern)
Mehr zur Compute-As-You-Think-Technologie
Wolfram-Predictive-Interface
Das Wolfram-Predictive-Interface bietet Ihnen eine vorausschauende Funktionsauswahl sowie Funktionsvorschläge für Ihre potenziell nächsten Schritte. Dieses neue Konzept beruht auf der Analyse von Millionen von Nutzeranfragen an die wissenschaftliche Suchmaschine Wolfram|Alpha.
Systeminterface und Portabilität
Systeminterface und Portabilität
Mathematica besteht aus zwei Teilen: dem Kernel, welcher die mathematischen Berechnungen vollzieht und die Programme ausführt, sowie einem "Front-End", das die Schnittstelle zum Anwender ist. Der Kernel arbeitet auf jeder Computerplattform gleich. Aus diesem Aufbaukonzept resultiert, dass sämtliche Softwarepakete, die mit Mathematica entwickelt wurden und werden, unter allen Computerplattformen austauschbar sind. Andererseits ist das "Front-End" so konstruiert, dass es die jeweiligen Möglichkeiten des Computers voll ausnutzt. Das "Front- End" und der Kernel brauchen nicht auf demselben Computer zu laufen. Alle Versionen sind untereinander voll kompatibel. So kann das "Front-End" auf einem Computer laufen und gleichzeitig per Netzwerk mit einem anderen Computer kommunizieren, auf welchem der Kernel installiert ist. Dies ermöglicht Anwendern den Zugriff auf die Geschwindigkeit von Supercomputern mit dem gewohnten Präsentationsstil eines PCs.
Spezielle Version von Mathemathica sind verfügbar als gridMathematica, webMathematica, Wolfram CDF-Player, siehe hierzu auch unser Mathematica-Varianten-Webseite.