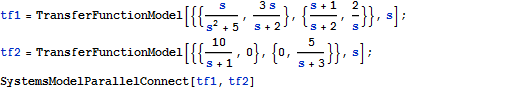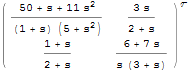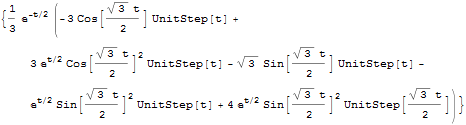Regelungstechnik
Seit Mathematica 8 können Regelungstechniker Steuer- und Regelungsmechanismen
berechnen, auswerten und dynamisch darstellen. Neben den weitreichenden numerischen
Methoden bieten die symbolischen Eigenschaften ungeahnte und noch nie da gewesene
Möglichkeiten, regelungstechnische Aufgaben zu simulieren.
- Statespace-Modelle
- Steuer- und Regelungstechnik mit integrierter Symbolfähigkeit
Die Bestandteile der Control-System-Pakete unterstützen Berechnungen in der Mechanik,
der Elektrotechnik, der Chemie, der Luft- und Raumfahrttechnik, der Biologie
und den Wirtschaftswissenschaften.
Analysieren und entwerfen Sie Steuerungen mit Hilfe von klassischen Techniken und Zustandsräumen, entwickeln Sie Lösungen für analoge und digitale Systeme und simulieren Sie Modelle in Konfigurationen mit offenen und geschlossenen Schleifen.
Einige Beispiele zu Control Systems:
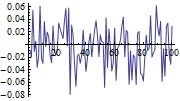
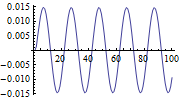
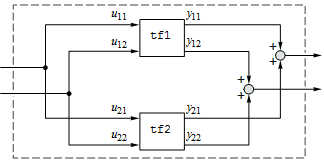
Zwei Parallelsysteme
Verbinden zweier Parallelsysteme
Sie erhalten das entsprechende Input-Output-Modell, indem Sie die beiden Systeme verbinden.
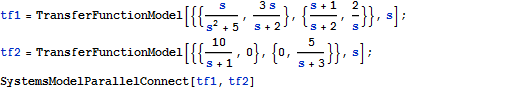
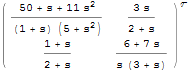
Interaktive Analyse
Interaktives Analysieren eines Systemverhaltens
Bestimmen Sie die kritischen Punkte des Systemverhaltens wie Break-Away, Break-In und Kreuzung der imaginären Achse mit Hilfe eines Root-Locus-Plots.

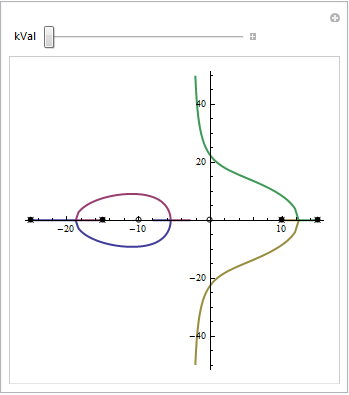
Systemstabilität
Bestimmen der Systemstabilität mit Hilfe der eingebauten Funktionen
Analysieren der Systemstabilität mit dem Nyquist-Plot:

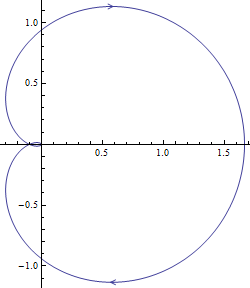
Visualisierungsmöglichkeiten
Visualisieren der relativen Stabilität des Systems
Amplituden- und Phasenreserve in einem Bode-Plot:

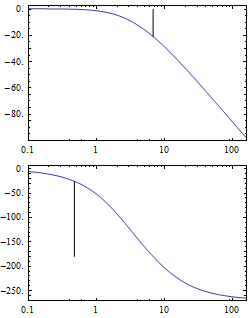
Frequenzgang
Bestimmen der Sprungantwort eines multivariablen Systems
Der "Singular-Value-Plot" einer Übertragungsfunktion:

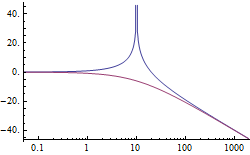
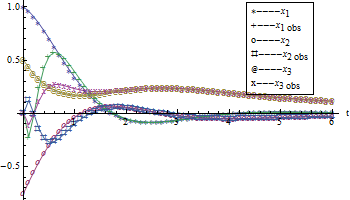
Beobachter und Regler
Erstellen von Beobachtern und Reglern zu einem bestimmten System
Abschätzen der Bahnen des Zustands und der Luenberger Beobachter:

Simulation
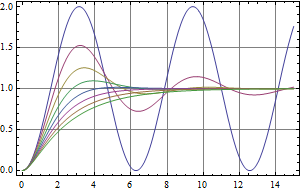
Simulieren der Antwort eines Zustandsraums oder einer Übertragungsfunktion
Die Sprungantwort eines Systems zweiter Ordnung für verschiedene Werte:
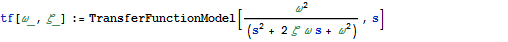

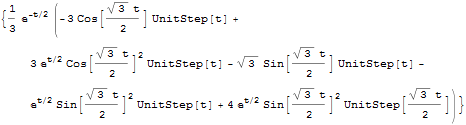

Kalman-Filter
Erstellen eines Kalman-Filters für ein stochastisches System
Ausgabe eines Filters vor und nach dem optimierten Filtern: