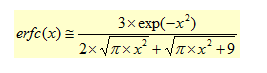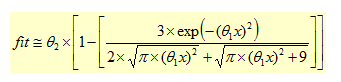Modellieren der Diffusion in einer Hochdruck-Entladungslampe (HID) mit Hilfe der nichtlinearen Regression in Minitab
Als ein Projektteam mit der Aufgabe, die Qualität und Zuverlässigkeit von Hochdruck-Entladungslampen bei Philips Turnhout zu testen, die chemischen Vorgänge einer neuen Generation von Produkten modellieren sollte, stellte es fest, dass Minitabs Funktionalität der nichtlinearen Regression den Zugang zur erweiterten Datenanpassung sehr einfach machte.
Von P. Watté, Philips Innovative Applications, Global Technology and Development HID & SL, Belgien
Einführung
Bei Philips Turnhout wird Minitab weithin für verschiedene Berechnungen eingesetzt, um die Qualität und Zuverlässigkeit von unseren HID-Lampen zu überprüfen und zu präsentieren. Kürzlich erkannte eines unserer Projektteams einen zusätzlichen Nutzen der in Minitab enthaltenen Optionen zur Modellanpassung. Insbesondere die Funktionalität der nichtlinearen Regression erleichtert den Zugang zu erweiterten Anpassungsprozessen erheblich. Wie in diesem Bericht dargestellt, wendeten wir sie an, um die chemischen Vorgänge innerhalb des Brenners einer neuen Generation von Produkten zu verstehen.
Philips hat eine neue Art Hochdruck-Entladungslampe entwickelt, die sogenannte Philips Mastercolour Evolution. Dieses revolutionäre Design verwendet Füllungen ungesättigten Metall-Halogens. Vorherige Generationen verwendeten für die Füllung eine zu große Menge an Salz, wodurch ein beträchtlicher Salzrückstand entstand, der die Leistung der Lampe beeinträchtigte. Das neue Lampendesign behebt dieses Problem. Folgerichtig ergeben sich nun ein “sauberer Strahl” und eine längere Lebensdauer der Lampe, da es kaum zu Korrosion des Aluminiumoxids im Brenner kommt. Abbildung 1 zeigt die untersuchte Lampe, eine Mastercolour Evolution 35 W T mit einem keramischen Lampensockel. Die Entladungsröhre verfügt über viel kleinere Stecker als eine klassische HID-Lampe aus dem Einzelhandel.
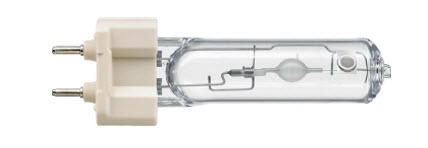 Abbildung 1: Die Lampe Mastercolour Evolution 35W T. Der Brenner ist der kugelförmige Teil innerhalb des Quarzgefäßes der Lampe.
Abbildung 1: Die Lampe Mastercolour Evolution 35W T. Der Brenner ist der kugelförmige Teil innerhalb des Quarzgefäßes der Lampe.
Problemstellung
Der Brenner (der kugelförmige Teil innerhalb der Lampe, in dem ein Plasma erzeugt wird) besteht aus polykristallinem Aluminiumoxid und wird mittels Spritzgussverfahren hergestellt. Unglücklicherweise können Elemente in Form von Oxiden aus der Brennermatrix diffundieren und reagieren mit der Salzfüllung. In den neuen ungesättigten Lampen stellt dies ein kritisches Problem dar. In diesem Artikel wird erläutert, wie wir mit der Diffusion eines bestimmten Elements (im Folgenden einfach als “X” bezeichnet) aus der Wand der Entladungsröhre umgingen.
Daten aus der hochauflösenden Spektroskopie
Wir schließen die technischen Informationen in diesem Abschnitt der Vollständigkeit halber mit ein. Leser, die sich nicht für diese Einzelheiten der Lampenherstellung interessieren, können diesen Abschnitt überspringen und bereits den nächsten Abschnitt lesen, in dem die Anpassung des Modells in Minitab erläutert wird.
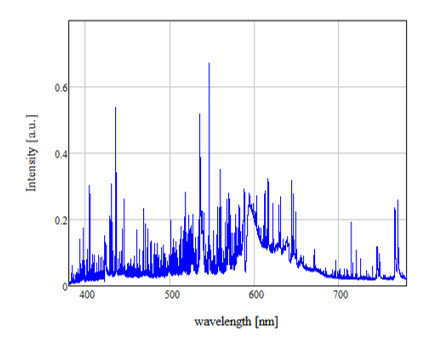
In der angewandten Lichttechnik kann die Entladungsröhre relativ hohe Temperaturen erreichen, genauer gesagt im Bereich 1500-1900 K. Dies fördert die Außendiffusion von Oxiden und anderen Elementen aus dem Brennermaterial. Die Menge dieser Elemente in der Entladung kann nicht direkt bewertet werden. Allerdings ist eine indirekte Bewertung durch die hochauflösende Spektroskopie möglich. Durch Zoomen in eine der Spektrallinien im hochauflösenden Spektrum können wir die vorhandene Menge des Elements X in der Entladung schätzen. Dies wird in Abbildung 2 gezeigt.
Die Außendiffusion von X aus dem Brennermaterial wird von einem temperaturabhängigen Diffusionskoeffizient bestimmt. Mittels der geeigneten Wahl einer Spektrallinie (wir normierten eine Spektrallinie von X auf eine Hg-Spektrallinie), wie in Abbildung 3 gezeigt, wird der Wert X/Hg an eine komplexe Fehlerfunktion erfc(x) angepasst. Dies stellt die allgemeine Lösung zu einer Diffusionsgleichung dar. Sechs Lampen des Typs Evolution 35W wurden nach 100, 500, 1000, 2000, 4000, 6000, 8000 und 10000 h gemessen. Der Boxplot der Werte X/Hg wird in Abbildung 4 dargestellt. Wir verwendeten diese Daten, um eine komplexe Fehlerfunktion anzupassen. Mathematische Softwarepakete können diese Aufgabe erfüllen. Es wird jedoch etwas mühsam, wenn Sie auch die Konfidenzgrenzen der Anpassung haben möchten.
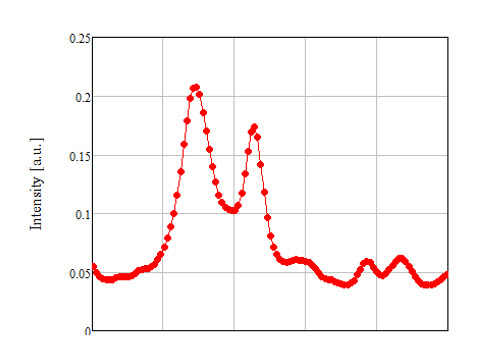 Abbildung 3: Vergrößerung einer Spektrallinie von X in dem hochauflösenden Spektrum. Die Wellenlängenskalierung wurde absichtlich weggelassen.
Abbildung 3: Vergrößerung einer Spektrallinie von X in dem hochauflösenden Spektrum. Die Wellenlängenskalierung wurde absichtlich weggelassen.
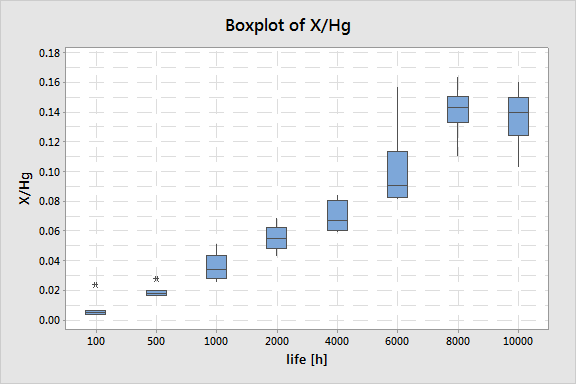 Abbildung 4: Boxplot der Entwicklung der dünnen optischen Linie von X relativ zu einer Hg-Linie als eine Funktion der Lampenlebensdauer. Jede Box stellt 6 Lampen dar.
Abbildung 4: Boxplot der Entwicklung der dünnen optischen Linie von X relativ zu einer Hg-Linie als eine Funktion der Lampenlebensdauer. Jede Box stellt 6 Lampen dar.
Datenanpassung in Minitab
Die Daten der hochauflösenden Spektroskopie wurden in zwei Spalten eines Minitab-Arbeitsblatt gespeichert, wie in Abbildung 5 gezeigt. Die erste Spalte enthält die Stunden der Lampenlebensdauer, bei denen die Messung durchgeführt wurde. Die zweite Spalte ist die Höhe der aufgezeichneten X/Hg-Werte. Minitab verfügt nicht standardmäßig über eine Funktion erfc(x), kann aber Minitab verwenden, um die Berechnung mit einer Approximationsformel von Abramowitz und Stegun durchzuführen.
Nun zu der Erklärung, wie elegant die Anpassung in Minitab durchgeführt wurde.
 Abbildung 5: Anordnung der Daten im Minitab-Arbeitsblatt. Spalte C1 ist die Lebensdauer der Lampe, bei der die HRS-Messung vorgenommen wurde. Spalte C2 ist das Verhältnis der dünnen, optischen X/Hg-Linien.
Abbildung 5: Anordnung der Daten im Minitab-Arbeitsblatt. Spalte C1 ist die Lebensdauer der Lampe, bei der die HRS-Messung vorgenommen wurde. Spalte C2 ist das Verhältnis der dünnen, optischen X/Hg-Linien.
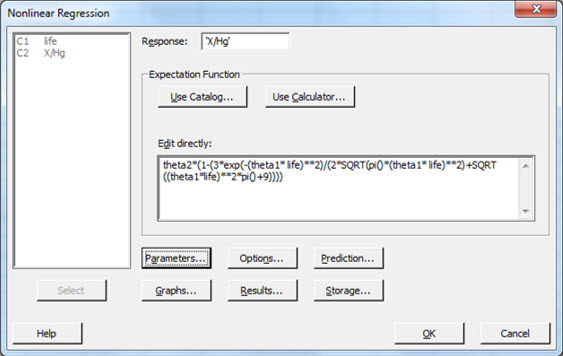
Um die erfc-Anpassung auszuführen, wählten wir im Menü Statistik Regression > Nichtlineare Regression…. Die Gleichung der Anpassungsfunktion muss in dem entsprechenden Fenster eingegeben werden. Nach der Minitab-Syntax müssen die Anpassungsparameter als θ1 und θ2 eingefügt werden, wie in Abbildung 6 gezeigt.
Beim Eingeben der Anpassungsfunktion ist es wichtig, die korrekte Anzahl von Klammern zu verwenden.
Die Anpassung wird mit Hilfe der folgenden Funktion durchgeführt:
Gleichung 2.
Wenn Sie auf ‘OK’ klicken, fordert Minitab Sie auf, zwei geschätzte Werte für die Fitparameter θ1 und θ2 einzugeben. Diese Anfangswerte werden in einem Levenberg-Marquardt- oder Newton-Gauss-Algorithmus verwendet, um die optimalen Anpassungswerte zu finden. Die grafische Ausgabe wird in Abbildung 7 dargestellt.
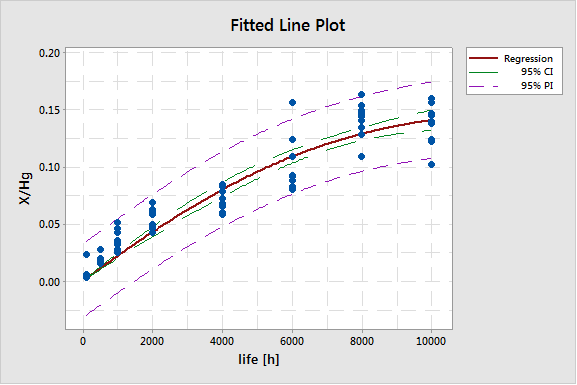 Abbildung 7: Fit der Anpassungsfunktion in Gleichung 2 an die HRS-Daten der Lampe CDM Mastercolour Evolution 35W als eine Funktion der Lebensdauer.
Abbildung 7: Fit der Anpassungsfunktion in Gleichung 2 an die HRS-Daten der Lampe CDM Mastercolour Evolution 35W als eine Funktion der Lebensdauer.
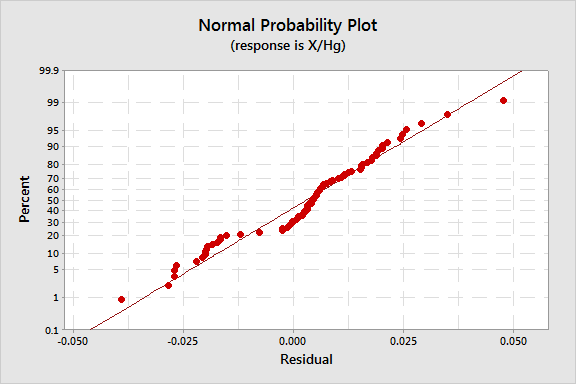
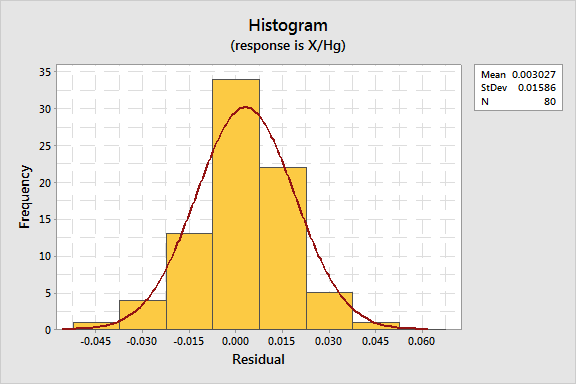
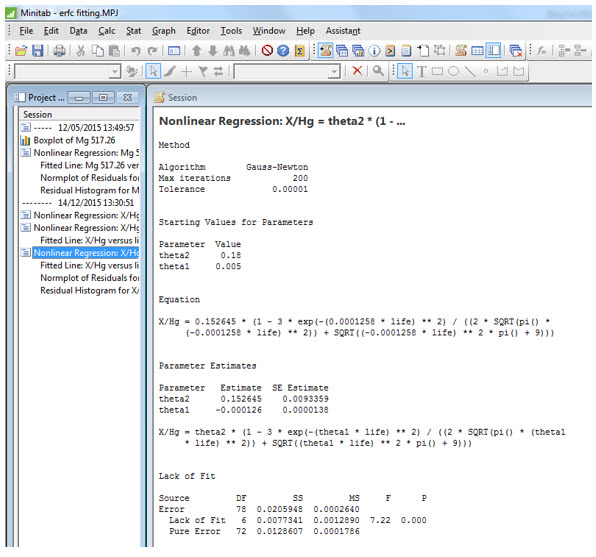
Schließlich können auch die Residuen gezeichnet werden und zwar in einem Wahrscheinlichkeitsnetz der Residuen (Normal) oder in einem Histogramm. Die Residuen sollten für eine qualitativ gute Anpassung einer Normalverteilung folgen. Dies ist hier offensichtlich der Fall, wie in den Abbildungen 8 und 9 zu sehen. Abbildung 10 zeigt das Session-Fenster, das nach der Anpassung angezeigt wird.
Abbildung 10 zeigt das Session-Fenster, das nach der Anpassung angezeigt wird. Es listet die Anpassungsparameter und ihre Standardfehler der Schätzung sowie eine Überprüfung auf eine fehlende Anpassung auf. Es zeigt weiterhin auf, dass wir den Newton-Gauss-Algorithmus zur Optimierung der Anpassung verwendeten. Bei den Anfangswerten θ1 = 0,005 und θ2 = 0,18 wurde die Lösung nach 11 Iterationen ermittelt.
Schlussfolgerung
Minitab wird bei Philips Turnhout weithin eingesetzt, um die Qualität und Zuverlässigkeit von HID-Lampen zu überprüfen und zu präsentieren. Wie oben beschrieben, entdeckte eines unserer Projektteams einen zusätzlichen Wert in der Verwendung der nichtlinearen Regression, um die chemischen Abläufe innerhalb des Brenners einer neuen Generation von Produkten zu verstehen. Das Team fand heraus, dass Minitabs Funktionalität der nichtlinearen Regression den Zugang zu erweiterten Anpassungsprozessen sehr vereinfachte.