Bayesian Estimation Tools für GAUSS
Das GAUSS-Paket "Bayesian Estimation Tools" beinhaltet sowohl vorgefertigte Modellschätzungen als auch Werkzeuge zum benutzerdefinierten Modellieren nach Bayes.
Funktionen
Vorgefertige Bayes-Analysen von Standard- und erweiterten Modellen
- univariate und multivariate lineare Modelle
- lineare Modelle mit autoregressiven Fehlertermen
- Hierarchische Bayes-Schätzung von Interaktionsmodelleln und gemischten Modellen
- Probit-Modelle
- Logit-Modelle
- Dynamische Faktormodelle mit zwei Faktoren
- SVAR-Modelle mit Optionen zu Beschränkungen der Vorzeichen (SVAR steht für Structural Vector Autogegressive).
Werkzeuge zur benutzerdefinierten Anpassung individueller Modelle
- Anzahl gespeicherter Iterationen
- Anzahl der zu übergehenden Iterationen
- Länge der Anlaufperioden
- Gesamtzahl der Iterationen
- Inklusion eines Intercepts
Laden und Erzeugen von Daten
Anwender können Daten zur Schätzung und Analyse in GAUSS mit den standardmäßig in GAUSS enthaltenen Prozeduren laden. Zusätzlich beinhaltet das Modul für die Bayes'sche Analyse jedoch eine Funktion zur Erzeugung von Daten, die es dem Anwender erlaubt, echte Datenparameter zu spezifizieren, um hypothetische Datensätze für die Analyse zu erzeugen.
Interpretation der gespeicherten Ergebnisse
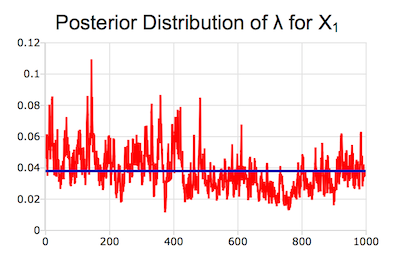
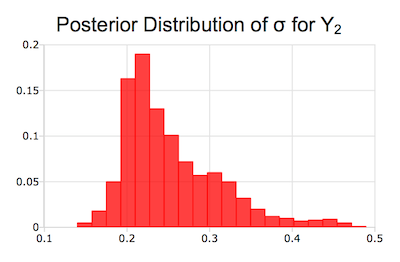
Die Bayes Estimation Tools speichern die Ergebnisse in einer einzigen Ausgabestruktur. Zusätzlich können alle Parameter und die Poseriori-Verteilungen für alle Parameter grafische dargestellt werden.
- Draws aller Parameter in jeder Iteration
- Posteriori-Mittelwert für alle Parameter
- Posteriori-Standardabweichung für alle Parameter
- Progostizierte Werte
- Residuen
- Korrelationsmatrix der prognostizierten und der beobachteten Werte
- Wahrscheinlichkeitsdichtefunktion und entsprechende Wahrscheinlichkeitsdichtefunktions-Gitter für alle Posteriori-Verteilungen
- Log-Likelihood (sofern anwendbar)
Beispiel
Beispiel: Bericht für ein Probit-Modell
Model Type: Probit regression model
*************************************************************
Possible underlying (unobserved) choice generation:
Agent selects one alternative:
Y[ij] = X[j]*beta_i + epsilon[ij]
epsilon[ij]~N(0,Sigma)
*************************************************************
Y[ij] is mvar vector
Y[ij] is utility from subject i, choice set j, alternative k
where i = 1, ..., numSubjects
j = 1, ..., numChoices
k = 1, ..., numAlternatives - 1
*************************************************************
X[j] is numAlternative x rankX for choice j
*************************************************************
Pick alternative k if:
Y[ijk] > max( Y[ijl] )
for all k < mvar+1 and l not equal to k
Select base alternative if max(Y)<0
*************************************************************
Observed model:
*************************************************************
Choice vector C[ij] is a numAlternative vector of 0/1
beta_i = Theta'Z[i] + delta[i]
delta[i]~N(0,Lambda)
*************************************************************
Summary stats of independent data
*****************************************
Summary stats for X variables
*****************************************
Variable Mean STD MIN MAX
X1 0.33333 0.47538 0 1
X2 0.33333 0.47538 0 1
X3 0.33333 0.47538 0 1
X4 0.28648 0.20641 -0.083584 0.71157
X5 0.083333 0.59065 -1 1
*****************************************
Summary stats for Z variables
*****************************************
Variable Mean STD MIN MAX
Y1 -0.10328 1.1582 -6.1714 3.7266
Y2 -0.23821 1.1428 -6.1295 3.2853
Y3 -0.28473 1.2776 -5.4752 4.58
*****************************************
Summary stats for dependent variables
*****************************************
Variable Mean STD MIN MAX
Y1 -0.10328 1.1582 -6.1714 3.7266
Y2 -0.23821 1.1428 -6.1295 3.2853
Y3 -0.28473 1.2776 -5.4752 4.58
***********************************
MCMC Analysis Setup
***********************************
Total number of iterations: 1100.0
Total number of saved iterations: 1000.0
Number of iterations in transition period: 100.00
Number of iterations between saved iterations: 0.0000
Number of obs: 60.000
Number of independent variables: 5.0000
(excluding deterministic terms)
Number of dependent variables: 3.0000
********************************
MCMC Analysis Results
********************************
***********************************
Error Standard Deviation
***********************************
Variance-Covariance Means(Sigma)
Equation Y1 Y2 Y3
Y1 0.20831 0.078641 -0.12772
Y2 0.078641 0.26217 -0.078051
Y3 -0.12772 -0.078051 1
***********************************
Error Standard Deviation
***********************************
Variance-Covariance Means (Lambda)
Equation Beta1 Beta2 Beta3 Beta4 Beta5
Beta1 0.038024 0.0084823 0.0050414 -0.010463 -0.0044786
Beta2 0.0084823 0.038058 0.0061952 -0.0098521 0.0017846
Beta3 0.0050414 0.0061952 0.080755 -0.0086755 0.016158
Beta4 -0.010463 -0.0098521 -0.0086755 0.10271 -0.010493
Beta5 -0.0044786 0.0017846 0.016158 -0.010493 0.046216
***********************************
Theta for Z Equation 1.0000
***********************************
Variable PostMean PostSTD
Theta1 0.53176 0.43012
Theta2 0.43195 0.35411
Theta3 -0.011848 0.00015526
Theta4 -2.0511 -1.9772
Theta5 1.0605 1.1038
***********************************
Theta for Z Equation 2.0000
***********************************
Variable PostMean PostSTD
Theta1 0.90016 0.79037
Theta2 0.37388 0.19278
Theta3 -0.32424 -0.37066
Theta4 0.69154 0.85307
Theta5 -0.26623 -0.19126
***********************************
Theta for Z Equation 3.0000
***********************************
Variable PostMean PostSTD
Theta1 -0.24998 -0.2454
Theta2 -0.22883 -0.19728
Theta3 -0.043585 0.026509
Theta4 -0.29718 -0.30046
Theta5 0.52032 0.50741
Systemvoraussetzungen
Systemvoraussetzungen
Betriebssysteme
- Windows
- Mac
- Linux
Voraussetzungen
- GAUSS ab Version 13.1