Statistik in OriginPro und Origin
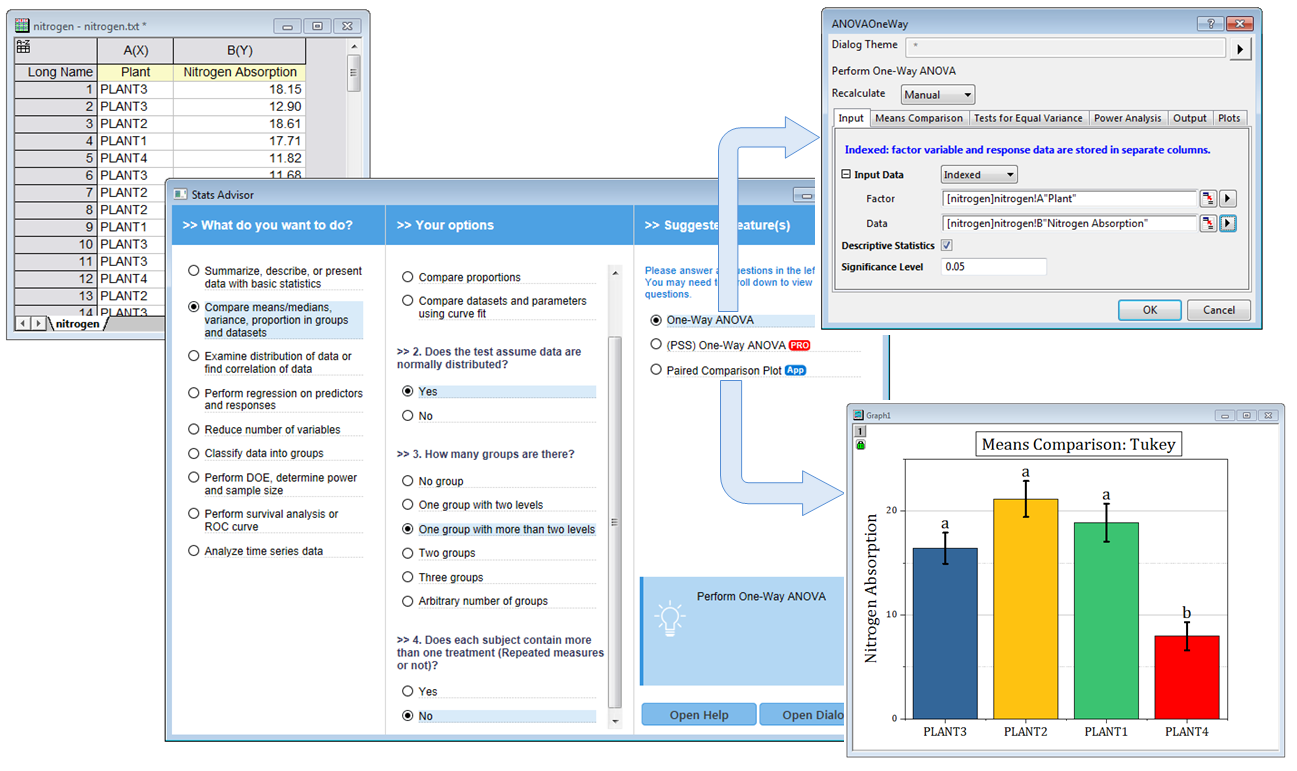
Die App Stats Advisor stellt eine Reihe von Fragen und schlägt dann das geeignete Hilfsmittel oder die geeignete App für die Analyse der Daten vor.
OriginPro und Origin bieten eine Vielzahl an Routinen, die sich für allgemeine statistische Analysen eignen, einschließlich deskriptiver Statistik, Hypothesentests bei einer oder zwei Stichproben sowie einfache und zweifache ANOVA. Zusätzlich werden mehrere Typen von statistischen Diagrammen unterstützt, wie beispielsweise Histogramme und Boxdiagramme.
Zusätzlich bietet Origin mit der App "Stats Advisor" ein Werkzeug an, das den Anwender interaktiv beim Wählen des passenden statistischen Tests, Analysehilfsmittels oder einer App unterstützt.
Außerdem stehen in OriginPro erweiterte statistische Analysehilfsmittel zur Verfügung, wie z. B. ANOVA bei wiederholten Messungen, ROC-Kurven (Receiver Operating Characterstic), Berechnungen von Trennschärfe und Stichprobenumfang und nichtparametrische Tests.

Die App Stats Advisor stellt eine Reihe von Fragen und schlägt dann das geeignete Hilfsmittel oder die geeignete App für die Analyse der Daten vor.
Deskriptive Statistik
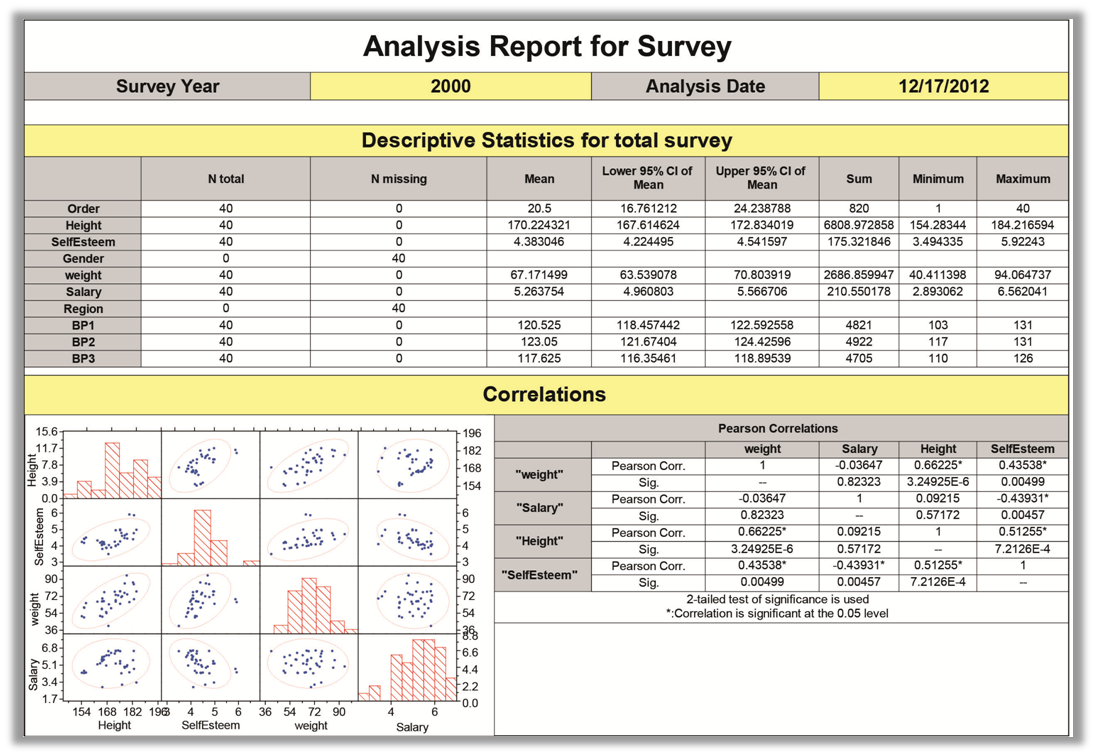
Die Abbildung zeigt einen benutzerdefinierten Bericht in Origin, der mit Origins flexiblem Arbeitsblatt erstellt wurde und numerische und grafische Ergebnisse von mehreren statistischen Hilfsmitteln anzeigt. Mit ihm können statistische Analyseaufgaben automatisiert werden.
In OriginPro und Origin stehen mehrere Hilfsmittel zur Verfügung, mit denen stetige und diskrete Daten zusammengefasst werden können:
- Spalten-/Zeilenstatistik
- KreuztabellePRO
- 1D- und 2D-Häufigkeitenzählung
- Diskrete Häufigkeit
- Test auf Normalverteilung
- VerteilungsanpassungPRO, einschließlich Normal, Weibull, Exponential und Gamma
- KorrelationskoeffizientPRO und teilweiser KorrelationskoeffizientPRO zum Erkennen von Beziehungen zwischen den Datensätzen
- Ausreißertests: Test nach Grubbs und Dixons Q

Die Abbildung zeigt einen benutzerdefinierten Bericht in Origin, der mit Origins flexiblem Arbeitsblatt erstellt wurde und numerische und grafische Ergebnisse von mehreren statistischen Hilfsmitteln anzeigt. Mit ihm können statistische Analyseaufgaben automatisiert werden.
Parametrische Tests
- t-Test bei einer Stichprobe
- t-Test bei zwei Stichproben und t-Test nach Welch
- t-Test bei verbundenen Stichproben
- t-Test auf Zeilen bei zwei StichprobenPRO
- t-Test auf Zeilen bei verbundenen StichprobenPRO
- Test auf Varianzen bei einer StichprobePRO
- Test auf Varianzen bei zwei StichprobenPRO
- Test von Anteilen bei einer StichprobePRO
- Test von Anteilen bei zwei StichprobenPRO
Nicht-parametrische Tests
- Wilcoxon-Rangtest mit Vorzeichen bei einer StichprobePRO
- Vorzeichentest bei verbundenen StichprobenPRO
- Wilcoxon-Rangtest mit Vorzeichen bei verbundenen StichprobenPRO
- Kolmogorov-Smirnov-Test bei zwei StichprobenPRO
- Mann-Whitney-TestPRO
- Kruskal-Wallis-ANOVAPRO
- Mood™-Median-TestPRO
- Friedman-ANOVAPRO
ANOVA
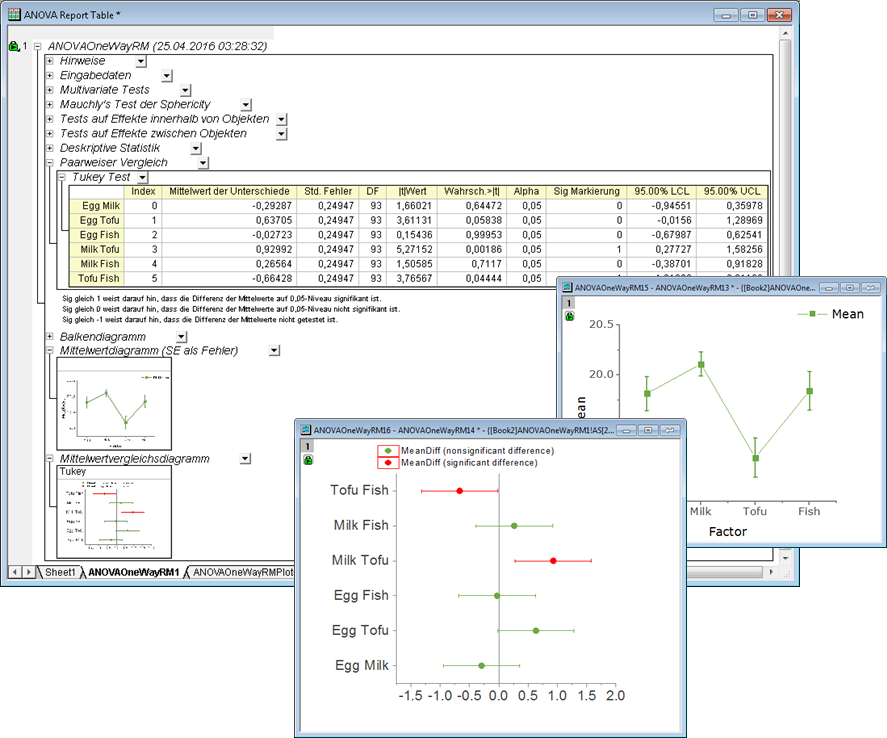
Ein Berichtsblatt von Origin, das mit dem Hilfsmittel Einfache ANOVA bei wiederholten Messungen erstellt wurde. Das Bild zeigt zwei der eingebetteten Diagramme, geöffnet zur weiteren Bearbeitung durch Doppelklick auf die Diagrammeinträge im Bericht. Die Diagramme können nach der Bearbeitung wieder in den Bericht eingefügt werden.
Origin verfügt über fünf Hilfsmittel für die ANOVA, um die Differenzen zwischen Gruppenmittelwerten zu untersuchen.
- Einfache und zweifache ANOVA
- Dreifache ANOVAPRO
- Einfache und zweifache ANOVA bei wiederholten MessungenPRO
- Methoden des Mittelwertvergleichs umfassen:
- Tukey und Bonferroni
- Dunn-Sidak und Fisher-LSD
- Scheffe und Holm-Bonferroni
- Holm-Sidak

Ein Berichtsblatt von Origin, das mit dem Hilfsmittel Einfache ANOVA bei wiederholten Messungen erstellt wurde. Das Bild zeigt zwei der eingebetteten Diagramme, geöffnet zur weiteren Bearbeitung durch Doppelklick auf die Diagrammeinträge im Bericht. Die Diagramme können nach der Bearbeitung wieder in den Bericht eingefügt werden.
Multivariate Analyse
In OriginPro können fünf gängige multivariate Hilfsmittel verwendet werden:
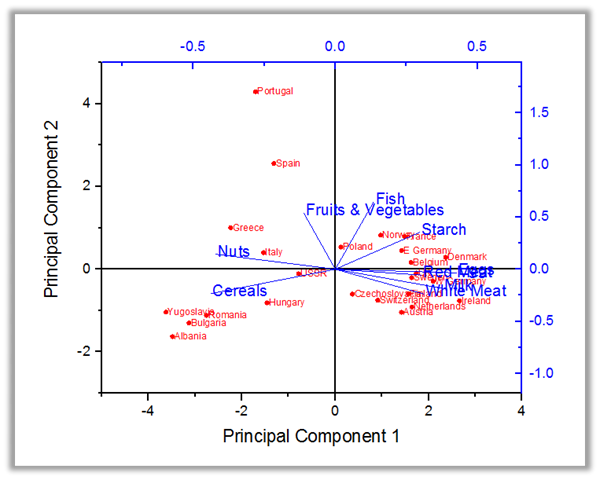
- Hauptkomponentenanalyse (PCA)PRO
- K-Means-ClusteranalysePRO
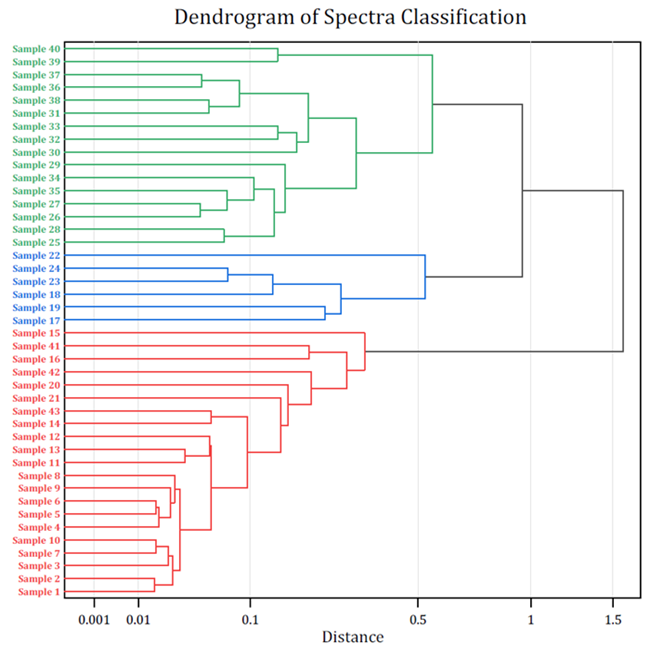
- Hierarchische ClusteranalysePRO
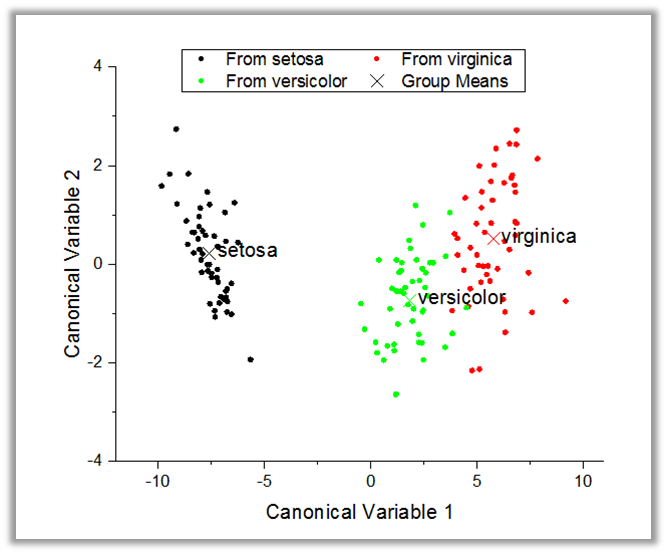
- DiskriminanzanalysePRO
- Partielle kleinste QuadratePRO
Zusätzliche Analysen
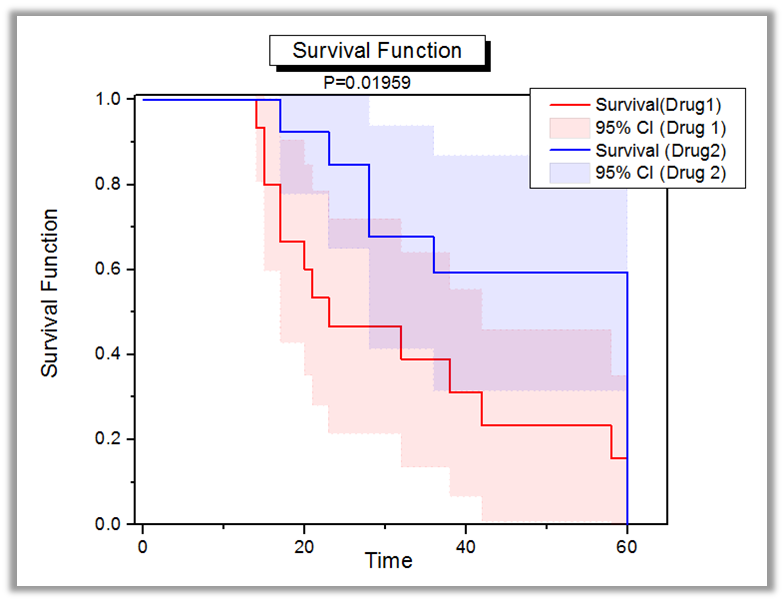
Dieses Diagramm zeigt die Lebensdauerfunktionen mit Konfidenzintervallen an, erstellt mit dem Hilfsmittel Lebensdaueranalyse in OriginPro. Das Hilfsmittel führt auch einen Log-Rang-Test durch, um die zwei Lebensaduerfunktionen zu vergleichen.
In OriginPro sind weitere statistische Hilfsmittel verfügbar:
- LebensdaueranalysePRO
- Trennschärfe und StichprobenumfangPRO
- ROC-KurvePRO